kd-Tree (Partition Trees)

• More like binary tree. Since we split region by 2 alternating between vertical and horizontal splits regardless of where points are. Until every point is in a separate region. This way of splitting gives range search to be more efficient.
• So each kd-tree keeps track of splitting line in one dimension.

kd-tree example:

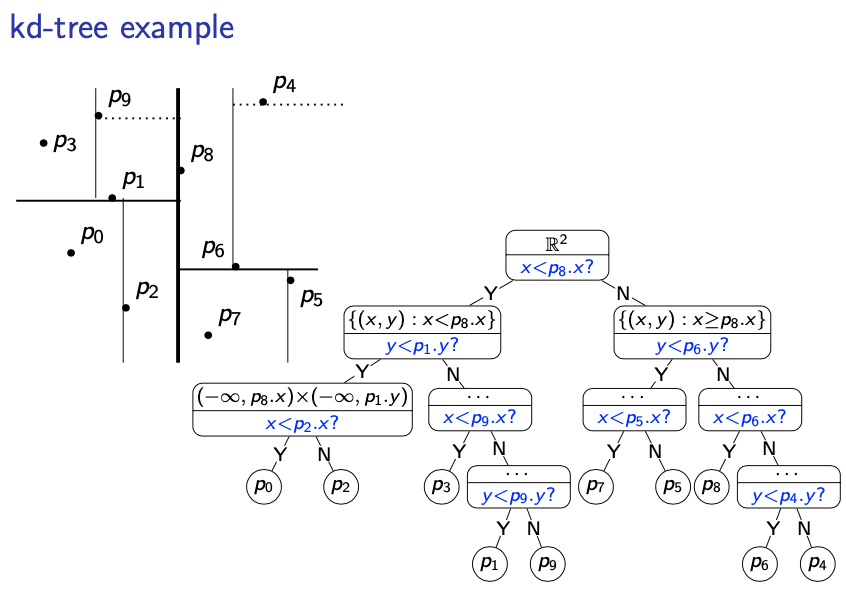
• No bounding box
• Root corresponds to the whole $R^2$
• First find the best vertical split
• $\lfloor \frac{n}{2}\rfloor$ on one side and $\lceil \frac{n}{2}\rceil$ and points on the other
• Recurse on the resulting regions (if they have more than one point)
• Alternate split direction

For example at the root, we have $x<p_8.x$ , then if the answer is Yes, we go left, if the answer is No, we go left. Next, we split vertically. And so on. We always split at a point.

Is the question at a node always $<$?

Constructing kd-trees

We build a kd-tree by initially splitting by x on points S:

• If $\left|S\right|\le 1$ create a leaf and return (only one point)
• Else $X=quickSelect(S,\lfloor \frac{n}{2}\rfloor )$ (select by x-coordinate)
• Partition $S$ by x-coordinate into $S_{x<X}$ and $S_{x\ge X}$
  • $\lfloor \frac{n}{2}\rfloor$ a points on one side and $\lceil \frac{n}{2}\rceil$ points on the other.
• Create left subtree recursively (splitting by y) for points $S_{x<X}$.
• Create right subtree recursively (splitting by y) for points $S_{x\ge X}$. Building with initial y-split symmetric.

Run-time:

• Find $X$ and partition $S$ in $\Theta (n)$ expected time using [randomized-quick-select], basically Quickselect.
• Both subtrees have $\approx \frac{n}{2}$ points.

$$T^{exp}(n)=2T^{exp}(\frac{n}{2})+O(n)$$

This resolves to $\Theta (n\log n)$ expected time

• This can be reduced to $\Theta (n\log n)$ [worst-case] time by pre-sorting (no details).

Height: $h(1)=0$, $h(n)\le h(\lceil \frac{n}{2}\rceil )+1$.

• This resolves to $O(\log n)$ (specifically $\lceil \log n\rceil$).
• Apparently this is not the expected height? You always take the median, so the height is deterministic. What does that mean (piazza 1233)

kd-tree Dictionary Operations

• $search$ (for single point): as in binary search tree using indicated coordinate
• $insert$: search, insert a new leaf
• $delete$: search, remove leaf

Problem:

• after insert and delete, the split might no longer be at exact median and the height is no longer guaranteed to be $\lceil {\log }_{2}n\rceil$.
• We can maintain $O(\log n)$ height by occasionally re-building entire subtrees. (No details.)
• kd-tree does not handle delete and insert well.

kd-tree Range Search

• Range search is exactly as for quadtrees, except that there are only two children (binary!!).

• We assume again that each node stores its associated region, (refer to above kd-tree example)

• To save space, we could instead pass the region as a parameter and compute the region for each child using the splitting line.

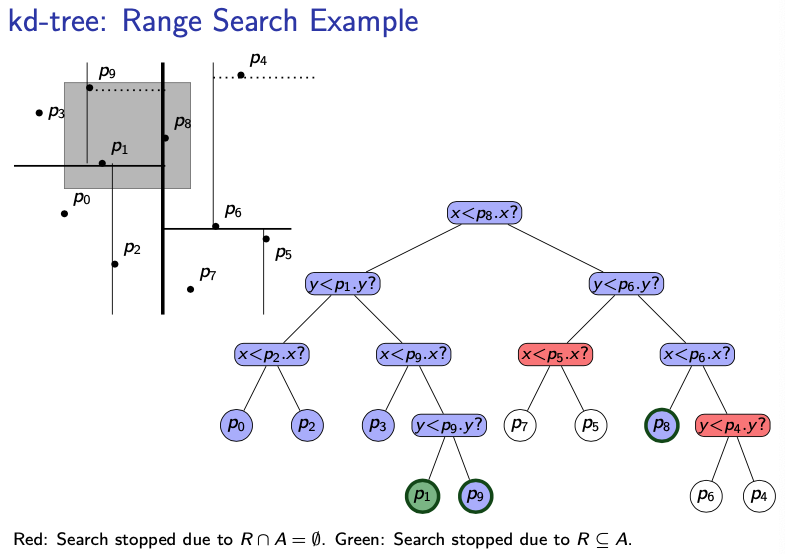
Range Search Complexity:

• The complexity is $O(s+Q(n))$ where → is this the same as $O(s+n^{1-1/d})$? Yes apparently from piazza.
  • $s$ is the output-size
  • $Q(n)$ is the number of “boundary” nodes (blue):
    • $kdTree::RangeSearch$ was called.
    • Neither $R\subseteq A$ nor $R\cap A=\varnothing$
• [Can show:] $Q(n)$ satisfies the following recurrence relation (no details):

$$Q(n)\le 2Q(n/4)+O(1)$$

• This solves to $Q(n)\in O(\sqrt{n})$ $\therefore$ the complexity of range search in kd-trees is $O(s+\sqrt{n})$ (that is if it’s 2-d)

For running time, enough to count blue nodes and add $O(s)$.

kd-tree: Higher Dimensions

Questions

What is the runtime of running a range search query on a 4-Dimensional kd-tree?

• The range search time is $O(s+n^{1-1/d})$, so if $d=4$, then it becomes $O(s+\sqrt[4]{n^3})$

The storage requirements for kd-trees in d-dimensional space is linear in n.

• True, said so in slides. To remember

It is impossible to design a comparison-based algorithm to build a kd-tree of size $n$ in worst case time $o(n\log n)$.

• True, violates the lower bound that says that any comparison-based sorting algorithm must make at least $\Omega (n\log n)$ comparisons to sort $n$ elements.

The height $h$ of a 2-dimensional kd-tree is never larger than the height of a 2-dimensional quad-tree where both trees store the same $n$ 2-dimensional points in general position (i.e. distinct $x$ and $y$ coordinates) and $h>0$.

• False, because a kd-tree splits into 2 subtrees, while a quad-tree splits into 4 subtrees, so it’s possible that the quad-tree will still have a smaller height.

The height $h(n)$ of a kd-tree for $n$ points, where $n$ is a power of 2, in general position satisfies the recurrence

$h(n)=h(n/2)+1$ At each level, the number of points is halved, and the height of the tree increases by 1. This is why the recurrence $h(n)=h(n/2)+1$ holds true for the height $h(n)$ of a kd-tree with $n$ points, when $n$ is a power of 2.

Suppose $Q(n)$ satisfies $Q(1)=1$ and $Q(n)=2Q(n/4)$, where $n$ is a power of $4$. Then:

• We can start by noticing the pattern in the recurrence.
• Given the recursive formula, we have:
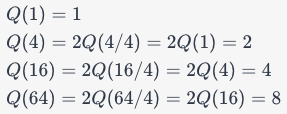
• As we can see, the values of Q(n) seem to be doubling with each step when $n$ is a power of 4. Specifically, $Q(n)=2^k$, where $k$ is the number of times we can divide $n$ by 4 until we reach 1. This is the same as the logarithm of $n$ to the base 4.
• Thus, the closed-form expression for $Q(n)$ is:

$Q(n)=2^{log{}_{4}n}=n^{1/2}$

Suppose during a range search on a 2-dimensional kd-tree with $n$ points that only 7 points were found within the given query rectangle. In the [worst case], the runtime to perform this range search is:

• $\Theta (\sqrt{n})$ , used the range search time on $d=2$.