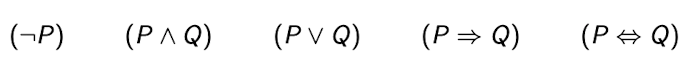Syntax
The syntax of a logic defines what is a “well-foremed formula” (wff).
Invented by George Boole.
Proposition symbols
A formula in propopsitional logic consists of the following symbols:
- Two constant symbols: true or false
- Prime proposition symbols
- Propositonal connectives
- Brackets
Propositional connectives

Syntax and well-formed formulas
Definition: The well-formed formulas (wff) of propositional logic are those obtained by the following construction rules:
- The proposition symbols, and constants, true and false, are formlas. Called atomic formulas
- If P and Q are wffs, then each of the following are formulas
Precedence

Associativity
Terminology

Formalizing natural languages
Definition: Proposition symbols represent declarative sentences. e.g. sentences that are true or false.
Pick the smallest declarative phrase without logical connectives, about which you can answer true or false. Use propositin symbols to represent these sentences, connect with propositional connectives.
Note: Refer to the Summary Page on Propositional Logic Formalization.
 al Formulas
al Formulas
Ambiguities in English
The use of logical connectives sometimes doesn’t exactly match their meaning in English.
”Unless” is OR