Probe sequence (many alternate slots)

Open addressing: Main idea: Avoid the links needed for chaining by permitting only one item per slot, but allowing a key $k$ to be in multiple slots.

[search] and [insert] follow a probe sequence of possible locations for key $k$: ⟨h(k, 0), h(k, 1), h(k, 2), …⟩ until an empty spot is found.

[delete] becomes problematic:

• Cannot leave an empty spot behind; the next search might otherwise not go far enough
• Idea 1: Move later items in the probe sequence forward.
• Idea 2: Lazy deletion: Mark spot as deleted (rather than null) and continue searching past deleted spots.

Linear probing

Simplest method for open addressing: linear probing $h(k,i)=(h(k)+i)$ mod $M$, for some hash function $h$. $\to$ basically is the calculation of going one cell forward and keep looking for an empty spot that you can put in

Look at linear probing example in notes.

Question

If the hash function spreads all keys uniformly, the search operation (using linear probing) has constant average-case running time if $\alpha$ is close to 1.

• False: When the load factor $\alpha$ is close to 1, it means that the hash table is almost full, and the number of elements is approaching the size of the hash table. In this case, collisions are more likely to occur, and linear probing may require probing through multiple occupied slots before finding an empty slot for insertion or searching. Now the average-case running time of linear probing depends on the probability of encountering a collision and how far we need to probe to find an available slot for the desired key. If $\alpha$ is close to 1, probability of collisions increases, leading to longer probe sequences on average. Thus slowing down both insertion and search operations.

Average-case running of linear probing

Is generally considered constant if the load factor is kept low, when $]alpha$ is significantly less than 1. IN such cases, the hash tables remains sparsely populated, and the probability of collisions and long probe sequences are minimized, leading to efficient constant-time average-case performance.

Implementing a dictionary with linear hashing may lead to $\Theta (n)$ runtime of insertion and searching.

• True, linear hashing is a dynamic hashing technique where the hash table is allowed to grow incrementally as elements are inserted. Resizing and rehashing occurs when the load factor $\alpha$ exceeds a certain threshold, we need to expand the table to add more elements. In the worst-case, when table undergoes resizing and rehashing, all elements need to be rehashed and moved to new positions in the expanded hash table. This operation can take linear time relative to the number of elements in the hash table, resulting in $\Theta (n)$ run-time for insertion and searching. But, with proper load factor management, hash table is periodically resized, achieving a constant time average-case performance!

Double hashing:

Double hashing is a collision resolution technique used in hash tables. It works by using two hash functions to compute two different hash values for a given key. The first hash function is used to compute the initial hash value, and the second hash function is used to compute the step size for the probing sequence.

(Independent Hash Functions)

• Some hashing methods require two hash functions $h_0,h_1$
• These hash functions should be independent in the sense that the random variables $P(h_0(k)=i)$ and $P(h_1(k)=j)$ are independent
• Using two modular hash-functions may often lead to dependencies.
• Better idea: Use multiplication method for second hash function: $h(k)=\lfloor M(kA-\lfloor kA\rfloor )\rfloor$,
  • $A$ is some floating-point number with $0<A<1$
  • $kA-\lfloor kA\rfloor$ computes fractional part of $kA$, which is in $[0,1)$
  • Multiply with $M$ to get floating-point number in $[0,M)$
  • Round down to get integer in {0,…,M-1}
• Some observations/suggestions:
  • Multiplying with $A$ is used to scramble the keys
  • Good scrambling is achieved with

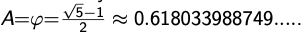
Double Hashing

• Assume we have two hash independent functions $h_{0,}{h}_1$
• Assume further that $h_{1(k)}\ne 0$ and that $h_1(k)\ne 0$
  • E.g. modifide multiplication method: $h(k)=1+\lfloor (M-1)(kA-\lfloor kA\rfloor )\rfloor$

[Double hashing: open addressing with probe sequence]

$$h(k,i)=(h_0+i\times h_1(k))modM$$

• search, insert, delete work just like for linear probing, but with this different probe sequence.

Example: (in notes)

• We calculate two results since we have two hash functions
• Which result do we use to insert into??????

Drawbacks:

• requires use of two hash functions, which can increase computational complexity of insertion and search operations
• requires good choice of hash functions for good performance. if not good, then collision rate is still high

Time Complexity??

• Insertion: $O(n)$
• Search: $O(n)$
• Deletion: $O(n)$

Auxiliary Space: O(Size of the hash table)