Trie

Also known as radix tree: A dictionary for bit-strings.

• Comes from retrieval
• A tree based on bitwise comparisons: Edge labelled with corresponding bit.
• Similar to radix sort: MSD-Radix Sort and LSD-Radix Sort.

Assumption: Dictionary is prefix-free: no string is a prefix of another

• Assumption satisfied if all strings have the same length
• Assumption satisfied if all string end with ‘end-of-word’ character $

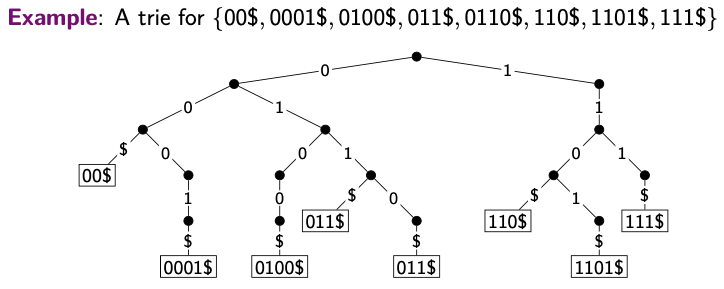
Then items (keys) are stored only in the leaf nodes.

Trie Search

• start from the root and the most significant bit of $x$
• follow the link that corresponds to the current bit in $x$ return failure if the link is missing
• return success if we reach a leaf (it must store $x$)
• else recurse on the new node and the next bit of $x$

Trie Insert

$Trie::insert(x)$

• Search for $x$, this should be unsuccessful
• Suppose we finish at a node $v$ that is missing a suitable child
  • Note: $x$ has extra bits left
• Expand the trie from the node $v$ by adding necessary nodes that correspond to extra bits of $x$

Does order of insertion matter? Will it give you the same compressed trie. $\to$ No, it shouldn’t matter

Trie Delete

$Trie::delete(x)$

• Search for $x$
• let $v$ be the leaf where $x$ is found
• delete $v$ and all ancestors of $v$ until we reach an ancestor that has two children

Time Complexity On all operations $\to \Theta (\left|x\right|)$ $\to$ length of the bit-string? Yes!

Questions

What is the runtime of searching for a string of size $l$ in an uncompressed trie that stores $n$ words over the alphabet $\sum$? (may assume that the children of a particular node are stored in increasing order by character in an array and that accessing a particular child takes $O(1)$ time.)

• $\Theta (l)$ , length of the string input, since all operations are $\Theta (x)$, where x is the input.

Inserting the same set of $n$ keys into a compressed trie will always result in a trie of the same height, regardless of the order they are inserted.

• True

The total number of nodes (given that we are storing $n$ words) in a standard trie is in $O(n+\sum _{wordsw}\left|w\right|)$

• True, why is it true?
• 1. Storing $n$ words: In a trie, each node represents a single character in the words being stored. The root node represents an empty string, and each subsequent node represents the next character in a word. So, the number of nodes needed to store $n$ words will be at least $n$ (one node for each character).

2. $\sum _{\text{words }w}\left|w\right|$: This represents the sum of the lengths of all the words being stored in the trie. In other words, it’s the total number of characters across all the words.

Related

• Patricia Trie - variant