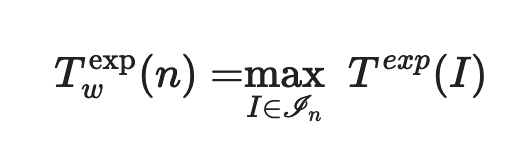Average Case Run-Time
Definition of average-case run-time:
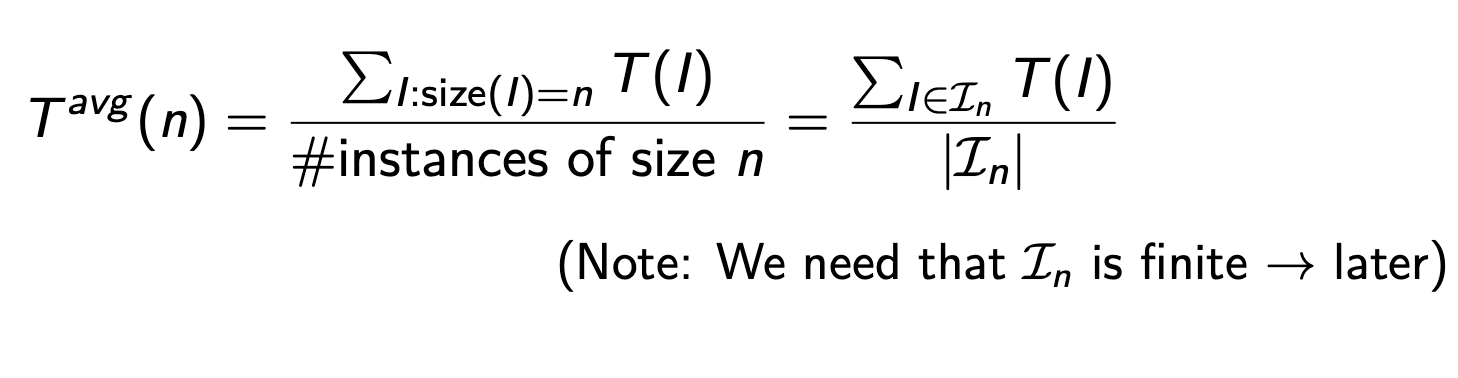
The average runtime refers to the actual observed running time of an algorithm over a specific set of inputs or executions. It is calculated by taking the sum of the individual runtimes and dividing it by the number of observations. The average runtime reflects the actual performance of the algorithm on the given inputs but does not consider any probabilistic behaviour or randomization
- Introduce (an solve) a new problem, then analyze the average-case run-time of our algorithm:

Claim: By induction: Ok for
- assume Ok for all integers less than .
- prove it for n:
-
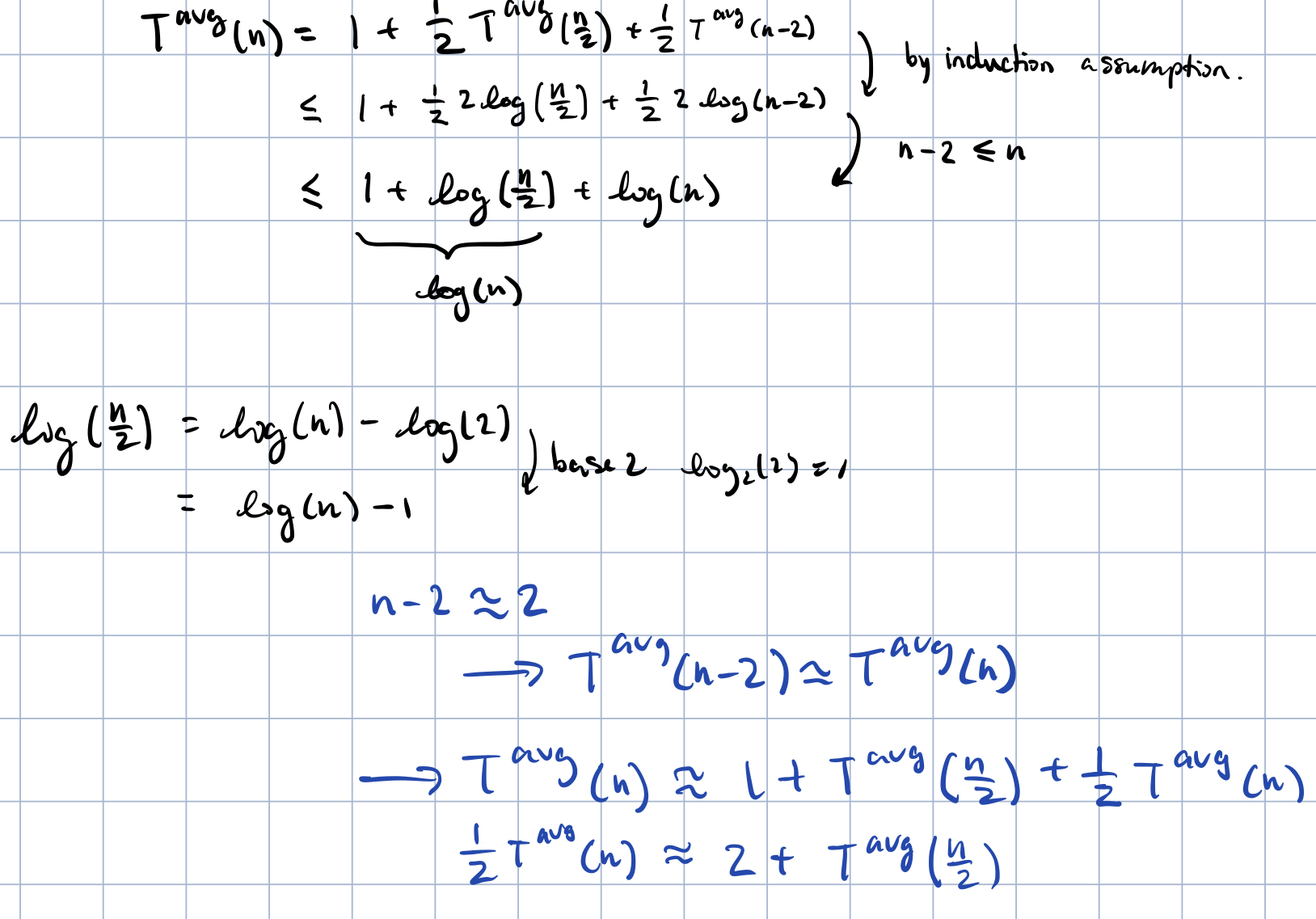
- What happened at the by induction assumption line?why turns to
- From claim that is ?
-
Questions
-
When do we calculate the expected running time of an algorithm as opposed to the average runtime?
- When we include randomization in the algorithm
- In such cases, the runtime of the algorithm can vary depending on the input data or random choices made during its execution. By calculating the expected running time, we can obtain an average estimation of the algorithm’s performance over a large number of executions or inputs.
- Randomized algorithms often rely on probabilities or random choices to achieve certain properties or improve efficiency. Examples of randomized algorithms include QuickSort with randomized pivot selection. Average run-time
-
We have provided the pseudocode for a game of Worthless. Your task is to answer the following multiple choice questions and use the results to derive the average running time for a single game.
define worthle_ss_guess(g): for i = 0 to n - 1: if g[i] == secret[i]: print ("Character {} matches", i) else: return "No match" end for return "The strings match. You've won!"- Recall the formula for the average runtime of an algorithm from the previous section. We need to first find the number of possible instances to the problem. Choose the correct option which represents the number of instances (i.e. the size of our input instance set).
- since each character in the guess can be one of the 26 letters and there are characters in total.
- How many guesses will fail on the first letter? (That is, how many possible entries will exit the for loop after comparing just the first character?)
- How many guesses will fail at the second character? (Think about what must have been true for the loop to complete one iteration.)
- Suppose that is the first index that the characters do not match (where ). What is the number of guesses which will result in a first-character mismatch at index ?
- , why is it
- How many guesses (input instances) will actually match with the secret word?
- Similar to how we approached these types of problems in Module 1, let us approach the runtime by counting the number of iterations started. Let be the first index at which the character comparison fails. Assuming represents the number of guesses that fail at index , what is the final expression for the average runtime of a single game of Worthless?
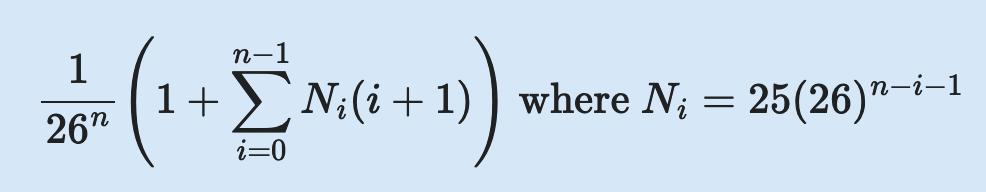
- is the number of comparisons for each instance. If you fail on index 0, then you’ve done 1 comparison, and so on.
- We will leave the math of simplifying the expression from the previous question as an exercise. What is the correct bound for the asymptotic runtime of a single game of Worthless, based on the final expression obtained after simplifying?
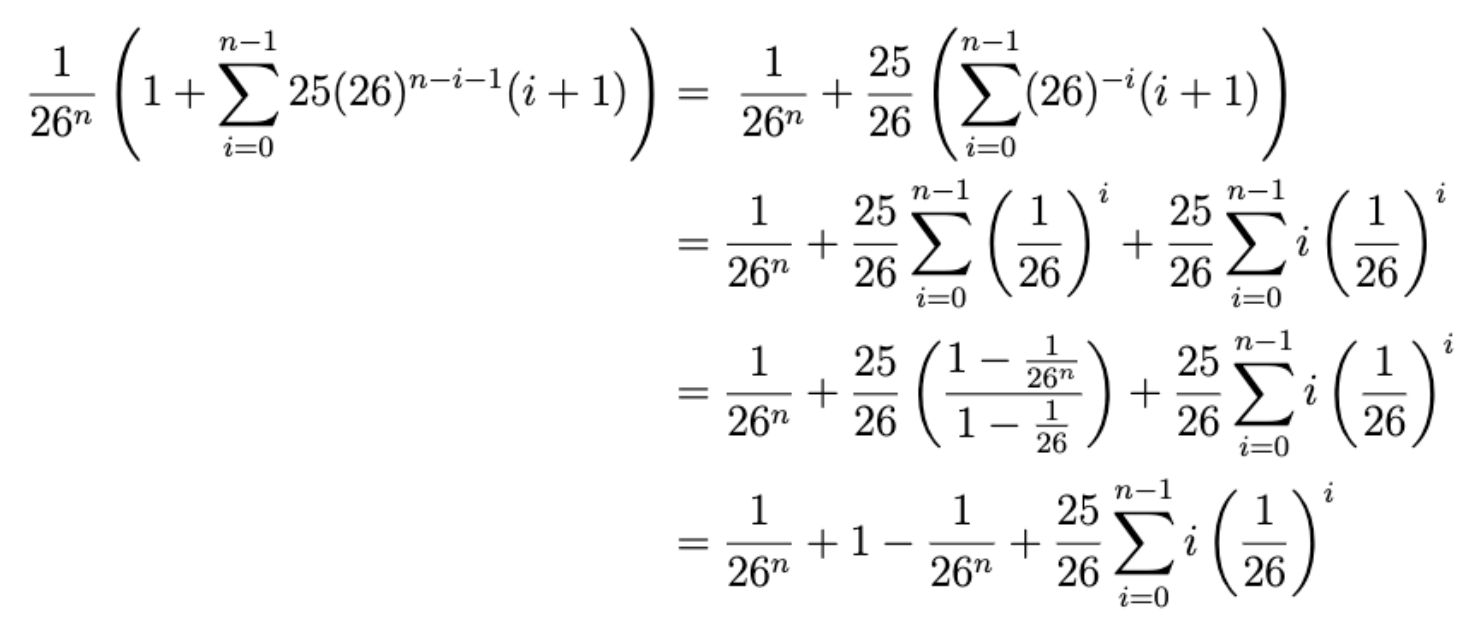
- Recall the formula for the average runtime of an algorithm from the previous section. We need to first find the number of possible instances to the problem. Choose the correct option which represents the number of instances (i.e. the size of our input instance set).
Expected Run-time Pseudocode
// A is an array of size n
// Each element is a unique number in the set {0,1,...,n-1}
// k is a positive integer in the set {0,1,...,n-1}
ArrayAlg(A, n, k):
i <- random(n) // You may assume this to be O(1)
if A[i] == k:
return i
else:
for j = 0 to n - 1:
print ("*")
end for
ArrayAlg(A, n, k)
end if- What is the absolute best-case time complexity for this pseudocode?
- , when and since is , overall we have .
- What is the absolute worst-case time complexity for this pseudocode?
- To deal with an infinite random sequence, we use the following equation: . What does represent? What values can it take?
- The current randomly generated index
- s the sequence of random values, as described in the question (and also in the lectures on randomized algorithms). We need this because the runtime of a randomized algorithm depends on the random values generated – the algorithm could be faster or slower depending on what random value it takes as an input. Every time we call the pseudorandom number generator, it consumes a value of this sequence we denote this value as , and the algorithm takes as an input.
- From the course notes, what is the expected running time on an arbitrary instance equal to?
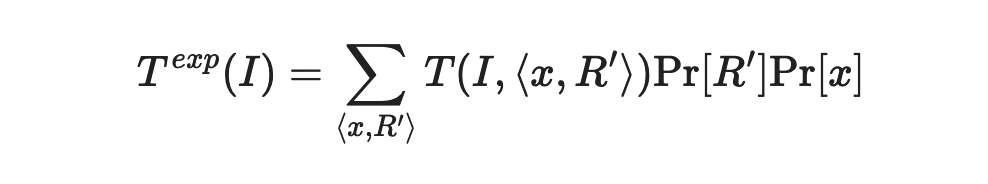
- What is the recurrence relation that represents the work done? Assume that an instance
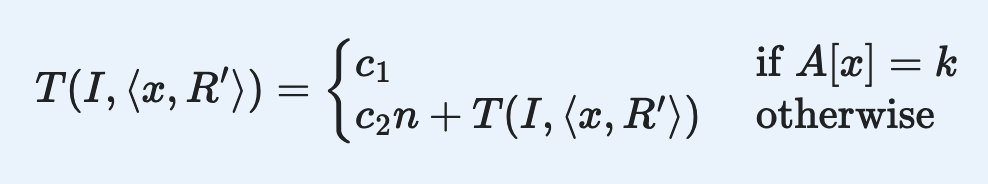
- Which of the following options best describes the worst-case expected running time of an algorithm?