Comparison-Based Algorithm

All sorting algorithms we’ve seen so far are comparison based algorithm which involves:

• comparing two elements
• moving

Examples of comparison-based algorithm:

• Quick Sort
• Heap Sort
• Merge Sort
• Selection Sort
• Insertion Sort?

Lower Bound for Comparison-Based Sorting Algorithm

Note

Theorem: Any correct comparison-based sorting algorithm requires at least Ω(n log n) comparison operations to sort n distinct items.

Claim: In a binary tree, for $h\ge 0$ , there are at most $2^h$ leaves of level (depth) at most $h$. Proof: if $h=0$, there is indeed at most $2^0=1$ leaf of level at most $0$. Otherwise, for $h>0$, we suppose this is true for $h-1$, and prove it for $h$. If the tree is just a root, there is $1\le 2^h$ leaf of level at most $h$, so we’re good. Else, all the leaves in our tree $T$ are either leaves in the left ($L$), or the right subtree ($R$) at the root. The leaves of level at most $h$ in $T$ have level at most $h-1$ in either $L$ or $R$, so by the induction assumption there are at most $2^{h-1}$ in $R$. This gives a total $\le 2^{h-1}+2^{h-1}=2^h$.

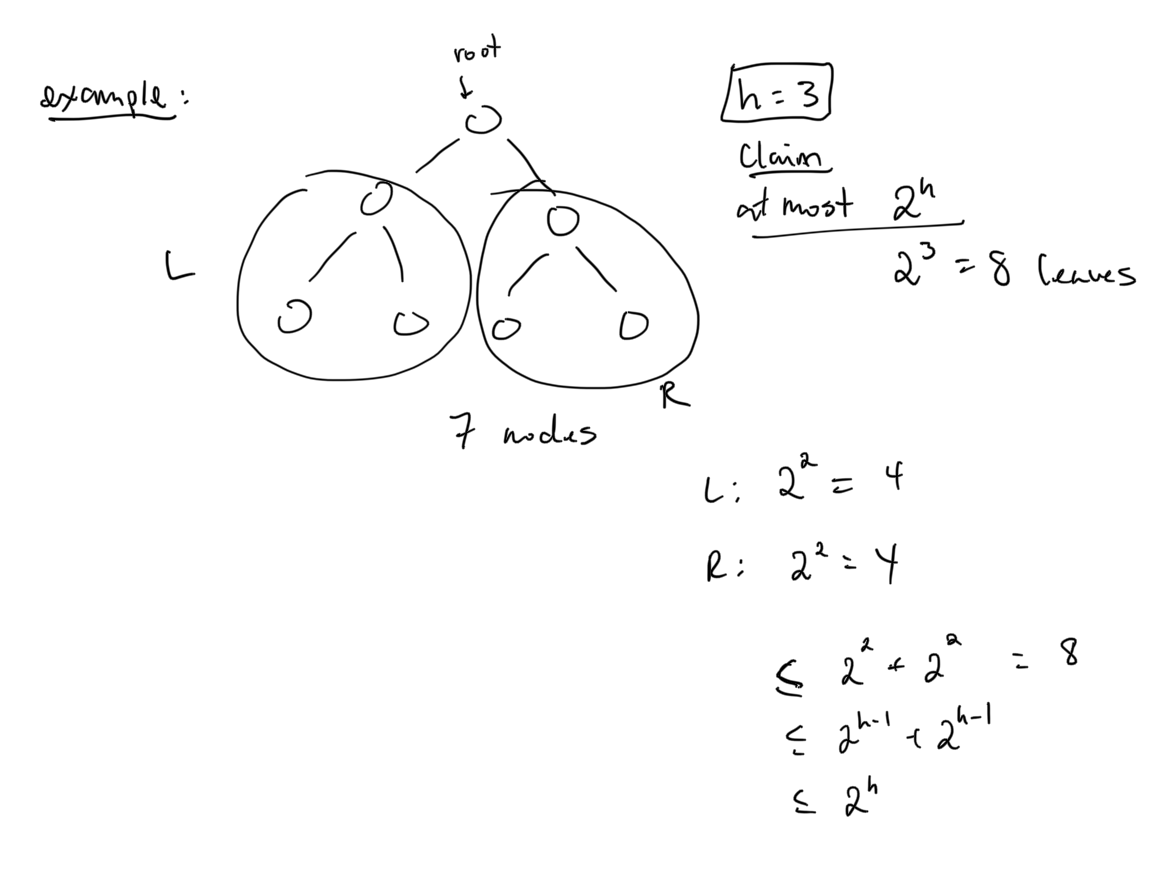
Claim: for any comparison-based sorting algorithm, the worst case number of comparisons for sorting arrays with distinct entries is $\Omega (n\log n)$. Proof: choose $n$ and consider the decision tree $T$ for our sorting algorithm in size $n$. There are $n!$ different input (=permutations of an array with distinct elements), so there are $n!$ leaves that can be reached from these inputs (labelled by $n!$ sorting permutations).

Remark

There could be more leaves, that cannot be reached from any input; we don’t care about them

Let $h$ be the maximal level of these $n!$ reachable leaves.

Important

This is also the worst case number of comparisons we’re doing in input size n.

All reachable leaves are at levels at most $h$, so by the claim above, there are at most $2^h$ of them. So: $n!\le 2^h$. Take a log: $h\ge \log (n!)$, so $h\in \Omega (n\log n)$, and we’re done.

Questions

• A comparison-based sorting algorithm (that returns the correct result for each instance) must have a best-case runtime that is $O(n\log n)$.
  • False
• It is not possible for a comparison-based searching algorithm to terminate in $o(\log n)$