Range Trees

Both Quadtrees and kd-Trees are slow for range searches. Quadtrees are also potentially wasteful in space.

Range trees are considered multi-dimensional range trees:

• organize dictionary points to support efficient $nD$ search with variant of BST search
• both internal and leaf nodes store points, similar to one dimensional BST

New idea: Range trees

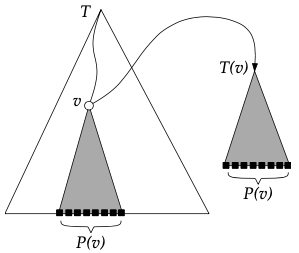
• Somewhat wasteful in space, but much faster in range search.
• [Tree of trees] (a multi-level data structure)

2-dimensional Range Trees

Primary structure: Balanced binary search tree $T$ that stores $P$ and uses [x-coordinate] as keys.

Every node $v$ of $T$ stores an [associate structure] $T(v)$:

• Let $P(v)$ be all points in subtree of $v$ in $T$ (including point at $v$)
• $T(v)$ stores $P(v)$ in a balanced BST using the [y-coordinate] as key.
• Note: $v$ is not necessarily the root of $T(v)$

Range tree example: 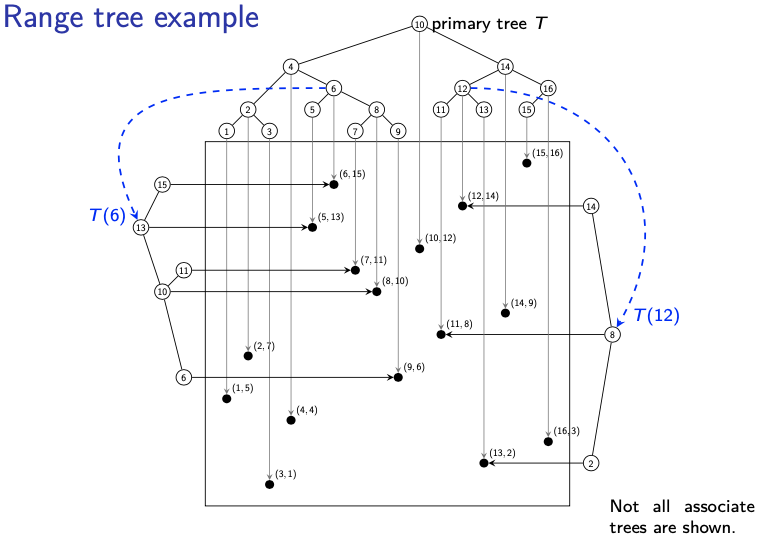Basically, each node $v$ has an associate tree (bst). But it is not shown in this picture. Only $T(12)$ and $T(6)$ are shown.

Range Tree Space Analysis

• Primary tree uses $O(n)$ space. How???

• Associate tree $T(v)$ uses $O(\left|P\right|)$ space, where $P(v)$ are points at descendants of $v$ in $T$

• Key insight: $w\in P(v)$ means that $v$ is an ancestor of $w$ in $T$

  • Every node $w$ has $O(\log n)$ ancestors in $T$ (Recall that we assume $T$ to be balanced)
  • Every node $w$ belongs to $O(\log n)$ sets $P(v)$
  • So $\sum \left|P(v)\right|\le \sum _{w}number-ancestors-of-w\in O(n\log n)$ $\therefore$ A range-tree with $n$ points uses $O(n\log n)$ space. $\to$ I think that’s because we have the initial primary tree with $n$ points and each one of them has an associated tree???

Range Tree Operations

• search: search by x-coordinate in $T$
• insert: First, insert point by x-coordinate into $T$. Then, walk back up to the root and insert the point by y-coordinate in all associate trees $T(v)$ of nodes $v$ on path to the root.
• delete: analogous to insertion

$\to$ Problem: We want the binary search trees to be balanced.

• This makes insert/delete very slow if we use AVL-trees (to balance, a rotation at $v$ changes $P(v)$ and hence requires to re-build $T(v)$

• Solution: Completely rebuild highly unbalanced subtrees (no details)

• $range-search$: search by x-range in $T$. Among found points, search by y-range in some associated trees.

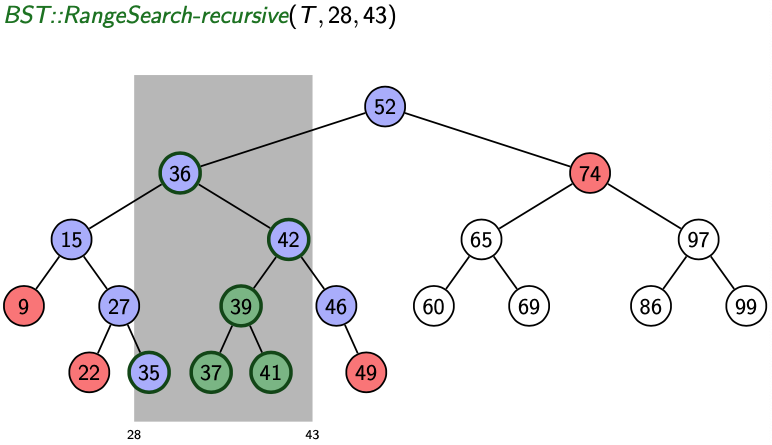
BST Range Search recursive Keys are reported in in-order (in sorted order)

BST Range Search example: Since $52>x_2=43$, we call recursion on the left, $r.left$ Now 36 is between $x_1$ and $x_2$, so we recurse on right subtree and left subtree. On the left subtree, $15<x_1=28$ so we recurse on the right. $27<x_1=28$ so recurse on the right. We arrive at leaf 35. On the right subtree, $42$ is between $x_1$ and $x_2$, so we recurse on both subtrees.

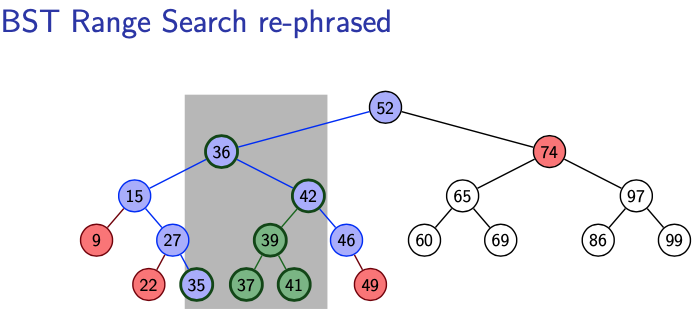
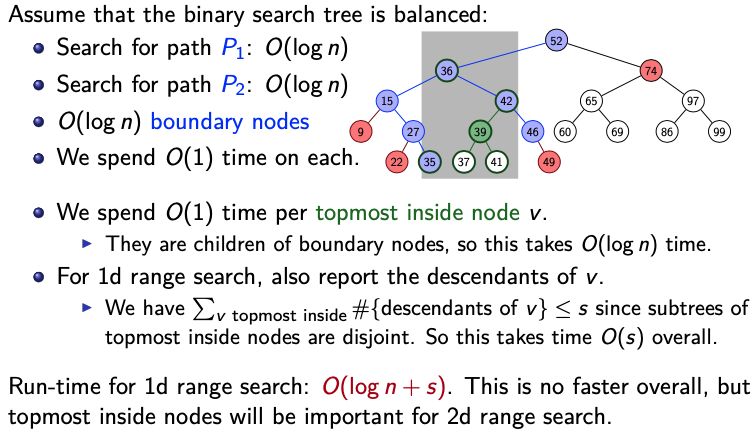
• Search for left boundary $x_1$: this gives path $P_1$ (By performing BST::search())

• Search for left boundary $x_2$: this gives path $P_2$ (By performing BST::search()) - This partition’s $T$ into three groups: outside, on, or between the paths.

• boundary nodes: nodes in $P_1$ or $P_2$

  • For each boundary node, test whether it is in the range. This is important, for each boundary node, we need to check explicitly if they fit in the range.

• outside nodes: nodes that are left of $P_1$ or right of $P_2$

  • These are not in the range, we don’t visit them

• inside nodes: nodes that are right of $P_1$ and left of $P_2$

  • We keep a list of the topmost inside nodes.
  • All descendants of such a node are in the range. For a 1d range search, report them.

BST Range Search Analysis

Range Trees: Range Search

Range search for $A=[x_1,x_2]\times [y_1,y_2]$ is a two stage process:

• Perform a range search (on the x-coordinate) for the interval $[x_1,x_2]$ in primary tree $T$ ($BST::RangeSearch(T,x_1,x_2)$
• Get boundary and topmost inside nodes as before.
• For every [boundary node], test to see if the corresponding point is within the region $A$.
• For every[ topmost inside node] $v$:
  • Let $P(v)$ be the points in the subtree of $v$ in $T$.
  • We know that all x-coordinates of points in $P(v)$ are within range.
  • Recall: $P(v)$ is stored in $T(v)$.
  • To find points in $P(v)$ where the y-coordinates are within range as well, perform a range search in $T(v):$ $BST::RangeSearchT(T(v),y_1,y_2)$

$P(v)$ are points in the subtree of $v$ in $T$ and it is stored in $T(v)$!

Example:

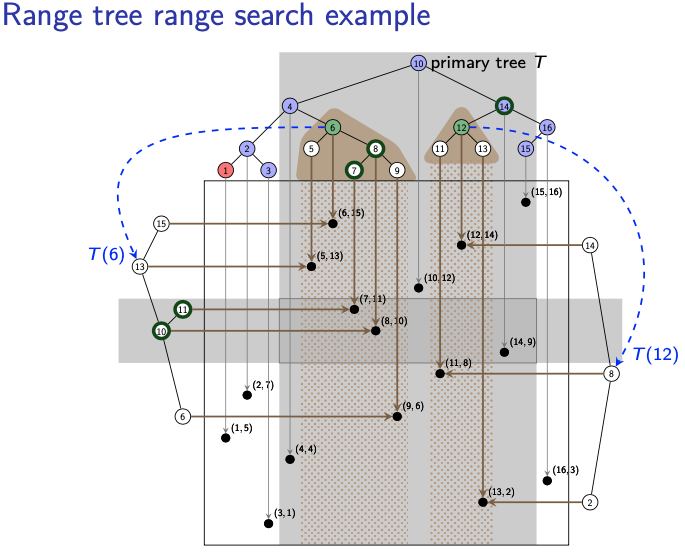
So my understanding, is that we start with x-coordinates, we found that the topmost nodes are 6 and 12. The boundary nodes are 4 and 14?? Is 15 also a boundary point? So we must test to see if the corresponding points are within the region, after checking 4 is not in region, but 14 is! Now I understand why we need to check boundary nodes. Then we go through the topmost nodes’s $P(v)$ and perform a range search in $T(v)$ to see where the y-coordinates are within range as well.

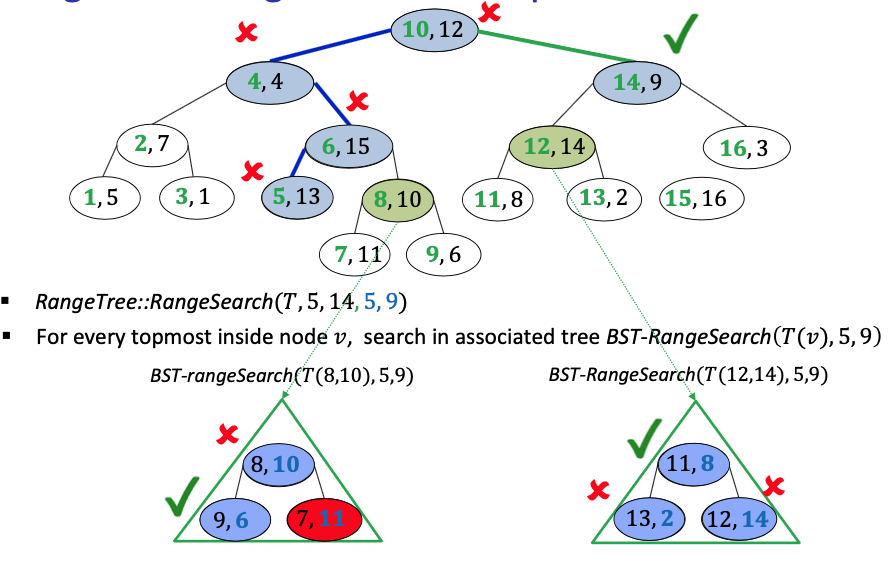
Overview:

• First perform only partial BST-RangeSearch
  • find boundary and topmost inside nodes which takes $O(\log n)$, but DO NOT go through the inside subtrees
  • modified version takes $O(\log n)$ time
    • does not visit all the nodes in valid range of BST-RangeSearch(T, 5,14)
• Next:
  • for boundary nodes, check if both x and y coord are in the range which takes $O(\log n)$ time as there are $O(\log n)$ boundary nodes
  • for every topmost inside node $v$, search in associated tree $BST::RangeSearch(T(v),5,9)$

Range Trees: Range Search Run-time

• $O(\log n)$ time to find boundary and topmost inside nodes in primary tree $T$. Since it’s similar to BST?
• There are $O(\log n)$ such nodes.
• For each topmost inside node $v$, perform range search for y-range in associate tree
  • $O(\log n)$ topmost inside nodes
  • let $s_v$ be the number of times returned for the subtree of topmost node $v$
  • running time for one search is $O(\log n+s_v)$ $\to O(\log n+s_v)$ time for each topmost inside node $v$, where $s_v$ is the number of points in $T(v)$ that are reported.
• Two topmost inside nodes have no common point in their trees $\Rightarrow$ every point is reported in at most one associate structure $\Rightarrow \sum _{v-topmost-inside}{s}_v\le s$

Time for range search in range-tree is proportional to

$$\sum _{v-topmost-inside}(\log n+s_v)\in O({\log }^{2}n+s)$$

It is ${\log }^2$ since it’s 2 dimensional.

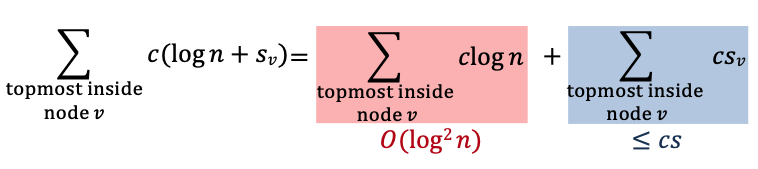
$\to$ Time for range search in range tree: $O(s+{\log }^{2}n)$

Range Tree Space Analysis

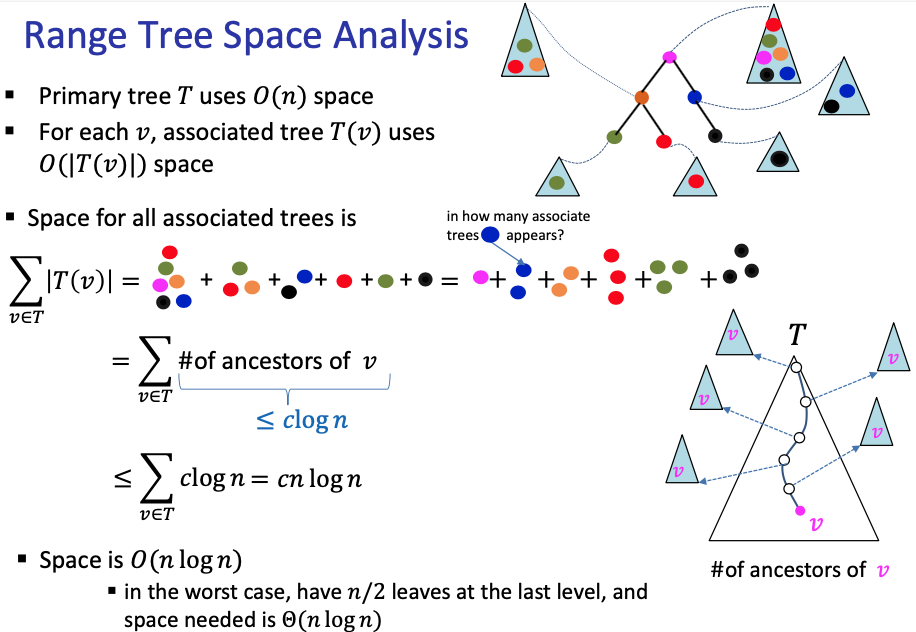
Basically to know the space taken for a range tree, we can think of it as the number of times each node appears in an associated tree which then equal to $\sum _v$ {ancestors of v } = $\sum _{v}O(c\log n)=cn\log n$. $\to$ Space is $O(n\log n)$

Higher Dimensions

Range trees can be generalized to d-dimensional space.

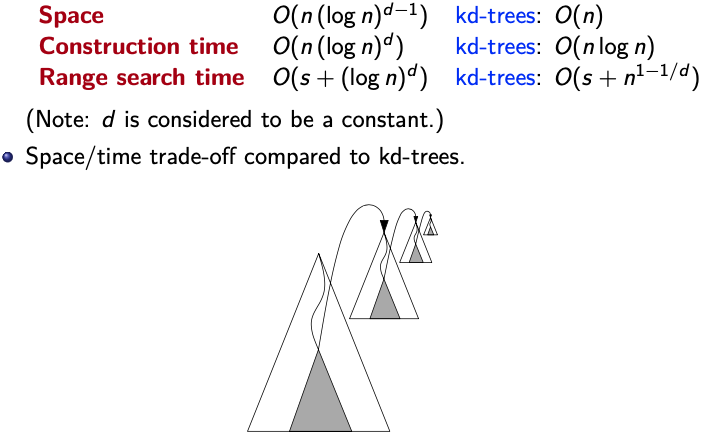
Range tree: Takes more space but better in range search, kd-Trees have less space but worse range search.

Summary

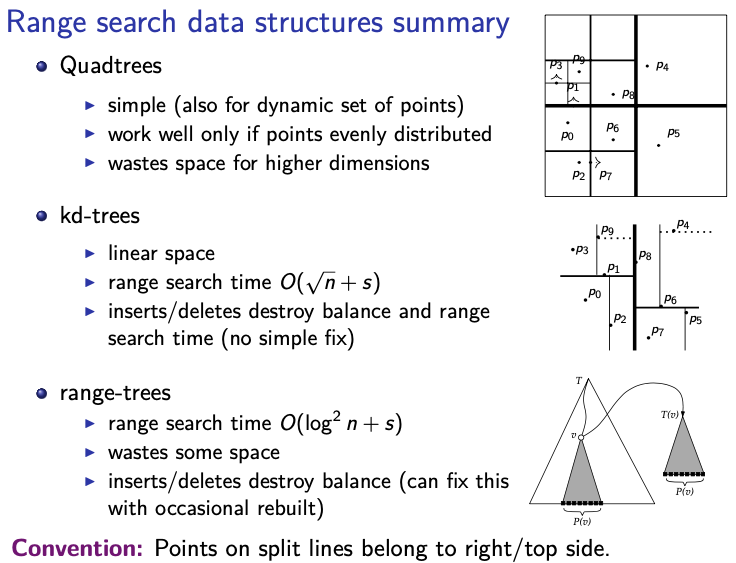
For Quad-tree, it can be space inefficient when two points are close to each other. Since $h=\Theta (\log \beta )$

Questions

In BST range search, there are always $\Theta (\log n)$ distinct inside nodes?

• False??

The best-case runtime of a 1-dimensional range search on a balanced binary search tree with $n$ nodes is:

• $\Theta (\log n)$ Worst case?
• $\Theta (n)$, so it is assumed that the BST is balanced, the run-time of the range search is hence $O(\log n+s)$. but if $s=n$ (i.e. all points are in range) then you can get a worse case $O(n)$ runtime. Now my question is how is it $O(n)$??
• I’ve asked on piazza

Suppose in 2D range tree storing n points the primary tree is not required to be balanced (ie. not required to have height O(log n)) but all associated trees are still required to be balanced. Does the worst-case asymptotic change? Give the largest possible number of nodes in a range storing n points. Briefly explain

• It will remain the same?