Directed Graphs

Directed Graph

$G=(V,E)$ as in the undirected case, with the difference that edges are (directed) pairs $(v,w)$

• edges are also called arcs
• usually, we allow loops, with $v=w$
• $v$ is the source node, $w$ is the target
• a path is a sequence $v_1,...,v_k$ of vertices, with $(v_i,v_{i+1})$ in $E$ for all $i$. $k=1$ is OK.
• a cycle is a path $v_1,...,v_{k,v1},k\ge 1$
• a directed acyclic graph (DAG) is a directed graph with no cycle

Directed Graphs basics

Definition:

• the in-degree of $v$ is the number of edges of the from $(u,v)$
• the out-degree of $v$ is the number of edges of the form $(v,w)$

Data structures:

• adjacency lists
• adjacency matrix (not symmetric anymore)

BFS and DFS for directed graphs

The algorithms work without any change. We will focus on DFS.

Still true:

• we obtain a partition of $V$ into vertex-disjoint trees $T_1,...T_k$
• when we start exploring a vertex $v$, any $w$ with an unvisited path $v⇝w$ becomes a descendant of $v$ (white path lemma)
• properties of start and finish times

But there can exist edges connecting the trees $T_i$.

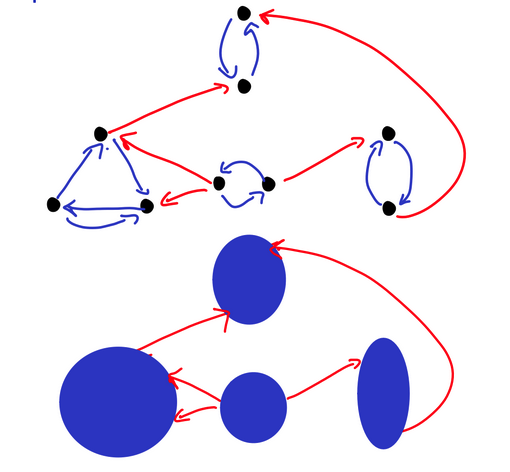
A directed graph G can be seen as a DAG of disjoint strongly connected components (SCC)

For any directed graphs, you will always be able to find its SCCs (even if that means its just a single SCC). Regardless, you will be able to create a DAG out of the SCCs

• See Korasaju’s Algorithm to find SCC of a directed graph.

Some questions:

• For a vertex $v$ in a directed graph $G$, are the neighbours of $w$ of vertex $v$ only the vertices where there is an edge from $v$ to $w$?
  • Yup, so the number of neighbours of $v$ in a directed graph $G$ is always equal to the out-degree of $v$.