Insertion Sort

Seen in CS341 - Algorithms textbook.

An efficient algorithm for sorting a small number of elements. Insertion sort works the way you might sort a hand of playing cards. Start with an empty left hand and the cards in a pile on the table. Pick up the first card in the pile and hold it with your left hand. Then, with your right hand, remove one card at a time from the pile, and insert it into the correct position in your left hand. You find the correct position for a card by comparing it with each of the cards already in your left hand, starting at the right and moving left. As soon as you see a card in your left hand whose value is less than or equal to the card you’re holding in your right hand, insert the card that you’re holding in your right hand just to the right of this card in your left hand. If all the cards in your left hand have values greater than the card in your right hand, then place this card as the leftmost card in your left hand. At all times, the cards held in your left hand are sorted, and these cards were originally the top cards of the pile on the table.

Algorithm

INSERTION-SORT(A,n)
	for i = 2 to n
		key = A[i]
		// Insert A[i] into the sorted subarray A[1: i - 1]
		j = i - 1
		while j > 0 and A[j] > key
			A[j+1] = A[j]
			j = j - 1
		A[j+1] = key

The pseudocode for insertion sort is given as the procedure INSERTION-SORT. It takes two parameters: an array $A$ containing the values to be sorted and the number $n$ of values of sort. The values occupy positions $A[1]$through $A[n]$ of the array, which we denote by $A[1:n]$. When the INSERTION- SORT procedure is finished, array $A[1:n]$ contains the original values, but in sorted order.

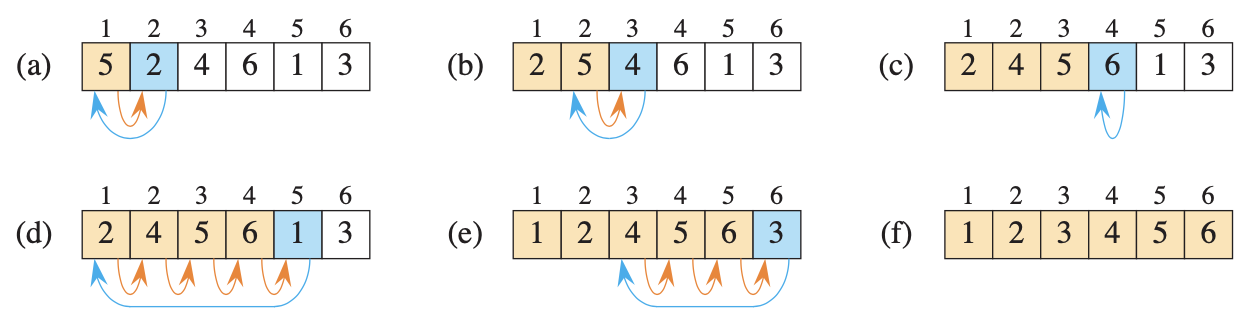
Analysis of Insertion Sort

How long does the Insertion Sort take? Depends on input size.

$$T(n)=c_{1}n+c_2(n-1)+c_4(n-1)+c_5\sum _{i=2}^n{t}_i+c_6\sum _{i=2}^n(t_i-1)+c_7\sum _{i=2}^n(t_i-1)+c_8(n-1)$$

The best case occurs when the array is already sorted and is given by:

$$T(n)=c_{1}n+c_2(n-1)+c_4(n-1)+c_5(n-1)+c_8(n-1)$$ $$=(c_1+c_2+c_4+c_5+c_{8)n}-(c_2+c_4+c_5+c8)$$

The worst case arises when the array is in reverse order - that is, it starts out in decreasing order.

$$\sum _{i=2}^{n}i=(\sum _{i=1}^{n}i)-1$$ $$=\frac{n(n+1)}{2}-1$$

and

$$\sum _{i=2}^n(i-1)=\sum _{i=1}^{n-1}i=\frac{n(n-1)}{2}$$

we find that in the worst case, the running time of insertion sort is

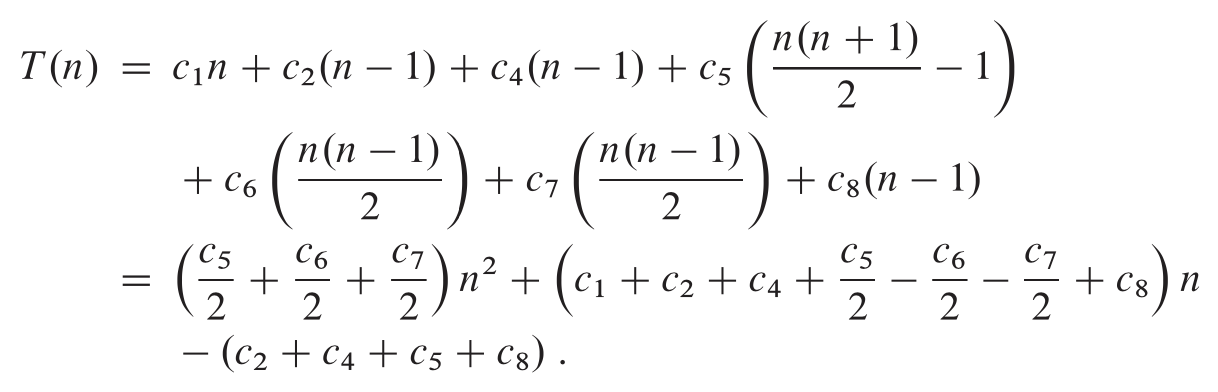
The running time is thus a quadratic function of $n$.

Average case: