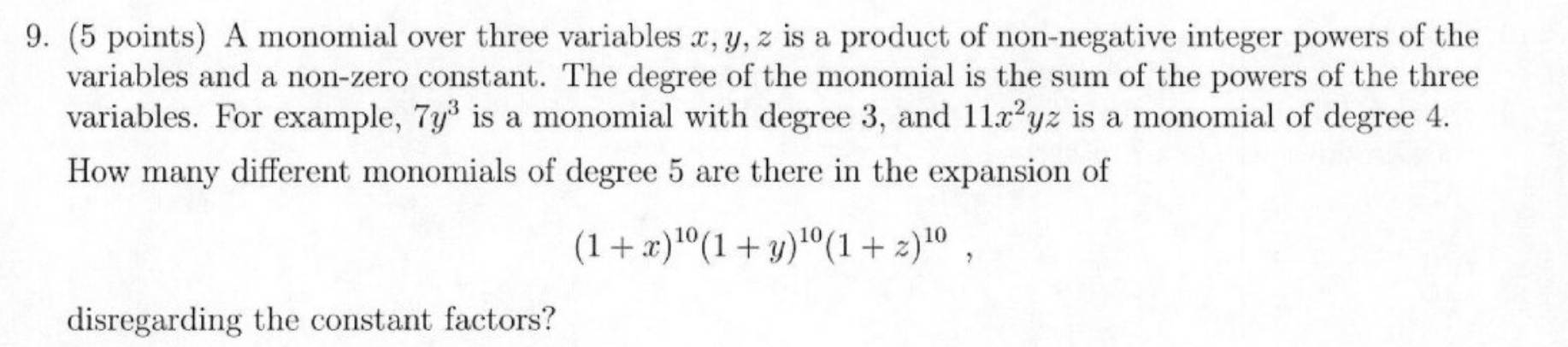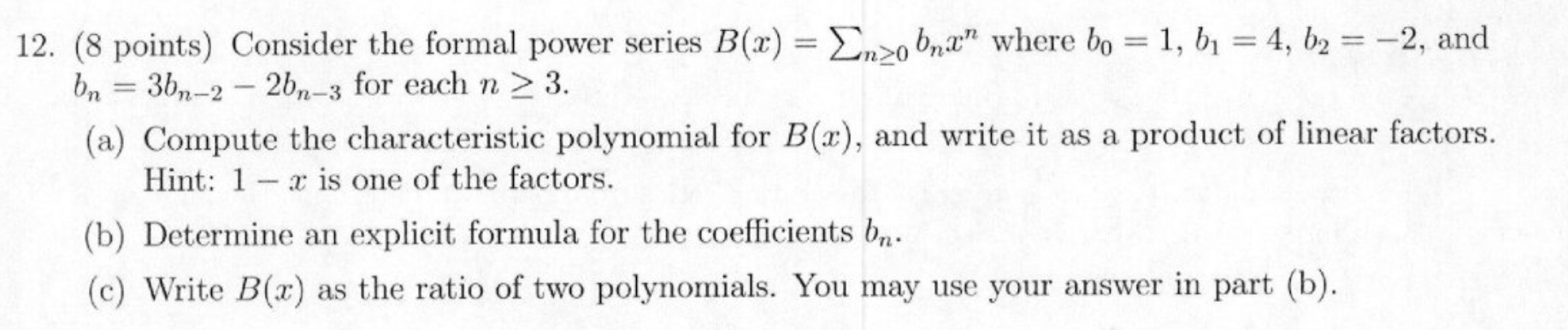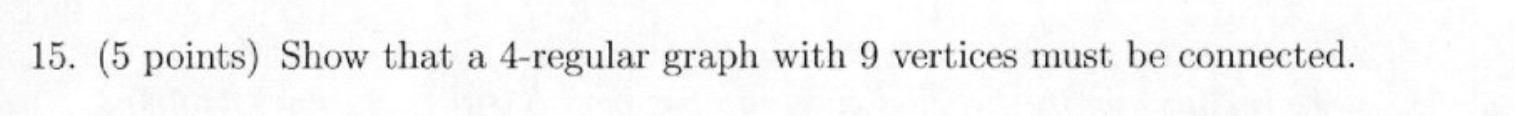MATH239: Introduction to Combinatorics

Taken in Summer 2023, taught by Douglas Stebila.

Not an easy course. With challenging weekly assignments.

Links:

• Some nice notes https://www.richardwu.ca/notes/math239-final-notes.pdf by Richard Wu

todo Will have to write my notes.

Resources:

• Math 239 Fall 2020 Lectures
• UW Math 239 Introduction to Combinatorics

Concepts

• Enumeration
• Graph Theory
• Hamiltonian Path
• Undirected Graph
• Eulerian Path
• Undirected Graph
• Tree
  • Spanning Tree
• Planar Graph
  • Euler’s Formula
  • Kuratowski’s Theorem
• Graph Colouring
• Graph Matching
  • Alternating Path and Augmenting Path
  • Bipartite Matching Algorithm
  • Konig’s Theorem
  • Hall’s Theorem
• Strong Connectivity

Final

Tip for final

I believe the key to mastering this final is being able to problem solve SUPER quickly. I struggled with the midterm for that. This is why you need to do lots of problems and just time yourself. Know the different theorems like the back of your hand, and when to use them. Build strong Intuition

Get good at induction. It seems that a lot of the proof require the use of induction.

Template for strong induction

• Inductive Hypothesis: Assume that $X$ holds for any tree/graph with less than m edges.
• Base Case: When $m=0,\dots ,$ so the result holds
• Inductive Step: …

Midterm

1-8. T/F and MCQ