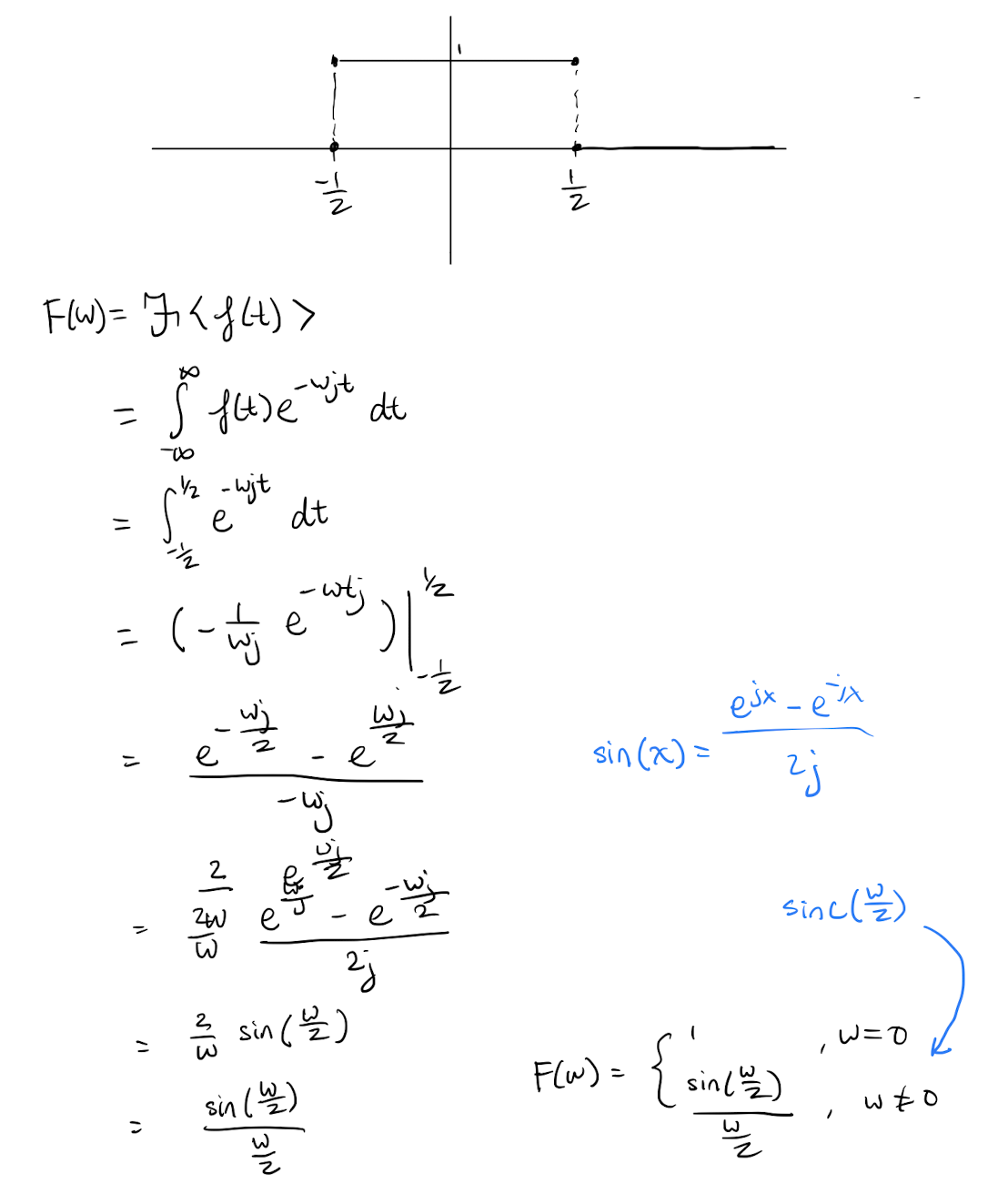
Fourier Transform (FT)

A Fourier transform is a mathematical transform that decomposes functions depending on space or time into functions depending on spatial frequency or temporal frequency.

Decompose it into pure frequencies.

It’s like unmixing different paint colours…

Take a pure signal. Converts time to frequency.

todo

Fourier transform (tldr;):

Recall that the two sided Laplace transform was defined by

$$\mathcal{L}\{f(t)\}={\int }_{-\infty }^{\infty }f(t)e^{-st}dt$$

given that the integral converged.

When working with (causal) DEs, we used the one sided version of the above.

In our work with Fourier series, we required that the functions be $\tau$ periodic. If this is not the case, then our methods do not work!!

What do we do with these cases? Recall

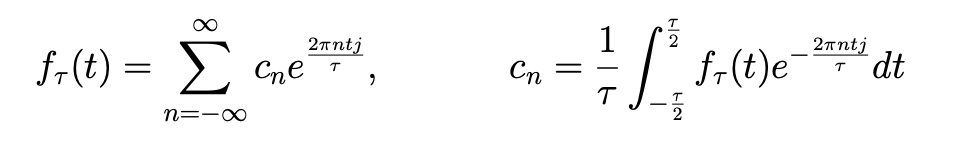
If $\tau \to \infty$ then $n$ is not allowed to be continuous so $c_n$ becomes a function of $\mathbb{R}$ and the discrete sum becomes an integral. Further we would need to do some regularization to deal with the averaging in $c_n$. Doing this defining $w$ to be the limiting values of $\frac{2\pi n}{\tau }$ (and some complex analysis to deal with the regularization) gives:

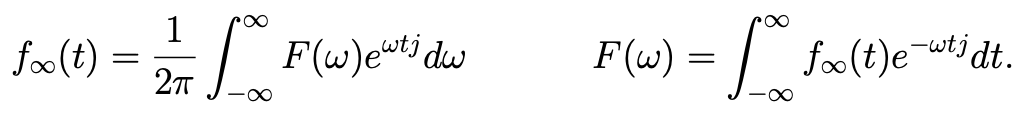
$F(w)$ is called the Fourier transform of $f_{\infty }$ and we write $F(w)=F\{f_{\infty }\}$ explicitly:

Definition 1: Fourier Transform

If $f\in L^1$ then the Fourier transform of $f$ is

$F(w)=F\{f(t)\}={\int }_{-\infty }^{\infty }f(t)e^{-wtj}dt$

and the inverse Fourier transform of $F(w)$ is

$f(t)=F\{F(w)\}=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }F(w)e^{wtj}dw$

Note that the Fourier transform/inverse transform is just the two-sided Laplace transform in the case that $s=wj$.