Asymptotic Analysis

”What doesn’t kill you, makes you stronger”

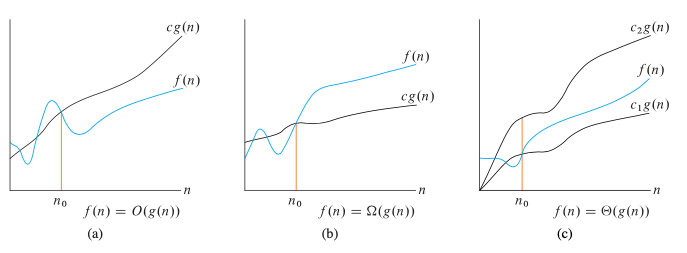
Smaller / Larger Asymptotic Bounds

Big-Oh

• $O-notation$: $f(n)\in O(g(n))$ ($f$ is asymptotically bounded above by $g$) if there exists constants $c>0$ and $n_0\ge 0$ such that $\mid f(n)\mid \le c\mid g(n)\mid$ for all $n\ge n_0$.

• So it suffices to show the existence of a single ($c$, $n_0$) pair.

• Gives asymptotic upper bound

  • $f(n)\in O(g(n))$ means function $f(n)$ is “bounded” above by function $g(n)$
    • eventually for large enough $n$
    • ignoring multiplicative constant
  • Growth rate of $f(n)$ is slower or the same as the growth rate of $g(n)$

• Use big-O to bound the growth rate of algorithm

  • $f(n)$ for running time
  • $g(n)$ for growth rate

• $\Omega -notation$

• $\Theta -notation$

big-Oh is only an upper bound

• typically example: 1 is in $O(n^2)$ and n is in $O(n)$
• try to give $\Theta$ ‘s if possibe

big-anything hides constants

• this is by design
• a $\Theta (n^2)$ will beat a $\Theta (n^3)$ algorithm eventually
• galactic algorithms: become practically relevant for astronomical input sizes (fast matrix or integer multiplication)

Asymptotic Lower Bound:

$f(n)\in \Theta (g(n))\iff f(n)\in O(g(n))andf(n)\in \Omega (g(n))$

• To prove that $f(n)\in \Theta (g(n))$, what do we need to show?
  • Separately showing that $f(n)\in O(g(n))$ and $f(n)\in \Omega (g(n))$?
  • Show ${\lim }_{n\to \infty }\frac{g(n)}{f(n)}=c,c\in \mathbb{R},c>0$
  • You need two constants $c_1$ and $c_2$ such that for all $n\ge n_0$, $c_{1}g(n)\le f(n)\le c_{2}g(n)$. The simplest way of showing this is to prove the two bounds separately and then take $n_0=max(n_{1,}{n}_2)$.

Summary of Order Notation

Strictly smaller/larger asymptotic bounds

$o-notation$

• We need to find an $n_0$ for each possible $c$. That is we find $n_0$, in terms of $c$. $\omega -notation$

Main difference to $O$ and $\Omega$ is the quantifier for $c$.

Rules of Order Notation

Transitivity:

• If $f(n)\in O(g(n))$ and $g(n)\in O(h(n))$ then $f(n)\in O(h(n))$.
• If $f(n)\in \Omega (g(n))$ and $g(n)\in \Omega (h(n))$ then $f(n)\in \Omega (h(n))$.

Maximum rules:

Suppose that $f(n)>0$ and $g(n)>0$ for all $n\ge n_0$. Then:

• $f(n)+g(n)\in O(max(f(n),g(n)))$
• $f(n)+g(n)\in \Omega (max(f(n),g(n)))$

Techniques for Order Notation

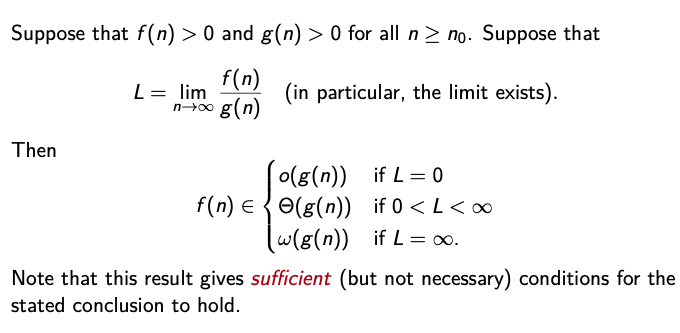
• Given two positive function $f(n)$ and $g(n)$ which asymptotic bounds can be proved/disproved directly using the Limit Rule?
  • $f(n)\in o(g(n))$
  • $f(n)\in \Omega (g(n))$
  • $f(n)\in \Theta (g(n))$
  • $f(n)\in \omega (g(n))$ Since the limit rule is only defined for $o$, $\omega$ and $\Theta$ bounds. It is true that if the $o$ bound is proven using the limit rule, then you have also shown an $O$ bound since $f(n)\in o(g(n))⟹f(n)\in O(g(n))$.

Common Growth Rates

• $\Theta (1)\to constant$
• $\Theta (\log n)\to logarithmic$
• $\Theta (n)\to linear$
• $\Theta (n\log n)\to linearithmic$
• $\Theta (n{\log }^{k}n)$ for some constant $k$ $\to quasi-linear$
• $\Theta (n^{2)}\to quadratic$
• $\Theta (n^3)\to cubic$
• $\Theta (2^{n)}\to exponential$

Relationship between Order Notations

• $f(n)\in \Omega (g(n))⟹f(n)\in \omega (g(n))$

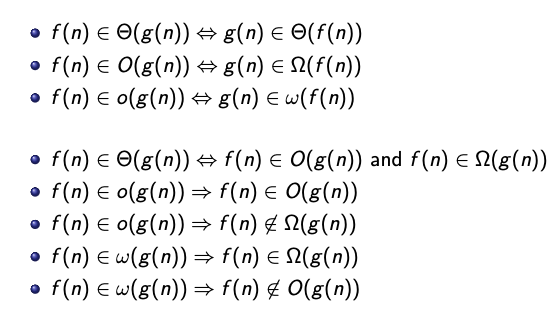
Questions

• $f(n)\in o(g(n))⟹f(n)\notin \Omega (g(n))$

  • true

• $f(n)\in \Omega (g(n))⟹f(n)\in \omega (g(n))$

  • false

• $f(n)\notin o(g(n))andf(n)\notin \omega (g(n))⟹f(n)\in \Theta (g(n))$

  • false

Choose the correct bound. Always select the bound which conveys the most information(the tightest bound)

• $84cos(2n^8-3n^3+n)\in \Theta (⨆)$
  • In $\Theta$ notation we are interested in finding a tight bound that represents the growth rate of the given function. The notation $\Theta (1)$ indicates that the function has a constant growth rate.
• $(\log (n+4){)}^{86}\in ⨆(n^{0.023})$
  • To determine the bound we take the limit of $f(n)$ and $g(n)$ and since it equals to $0$, from the definition, we know that $f(n)$ grows slower than $g(n)$, so we have $(\log (n+4){)}^{86}\in o(n^{0.023})$.
• $5^n\in ⨆(2^n)$
  • By taking the limit of $n$ approaching $\infty$, we see that it’s equal to $\infty$, so we have $5^n\in \omega (2^n)$
• $3^n\in ⨆(n!)$
  • By taking the limit of $n$ approaching $\infty$, we see that it’s equal to $0$. Thus, we have $5^n\in o(2^n)$.
• $2^n\in \Theta (⨆)$
  • $\frac{2^{e\ln n}}{3}+89n^2$

Which of the followings is in increasing order of growth rate?

• $(\log n{)}^3$, $n(\log n{)}^3$, $n^3$,$n^3\log n$, $3^n$

Note

$n^3\le n^3\log n$

Which one is true?

• $T(n)=2T(\frac{n}{2})+\Theta (n)⟹T(n)\in \Theta (n\log n)$
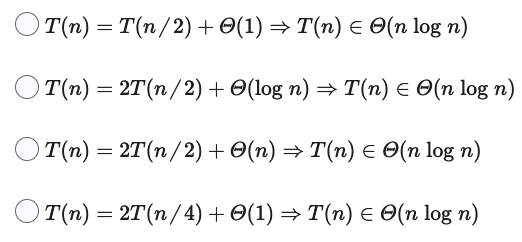
• Look at Recurrence Relations

In the Random Access Machine (RAM) model, which of the following is not true?

• The assumptions made in the RAM model are also true for real computers (false)
• Access to a memory location takes constant time. (true)
• Running time of a program is proportional to the sum of the number of memory accesses and primitive operations. (true)
• Primitive operations take constant time. (true)