Q1:
a):
We can use straight-line depreciation to find a depreciation rate of 5000 per year. BV and depreciation schedule is as follows:
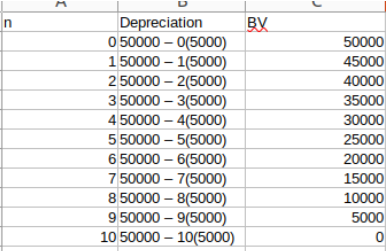
b)
With declining-balance depreciation, the depreciation schedule and BV are here:
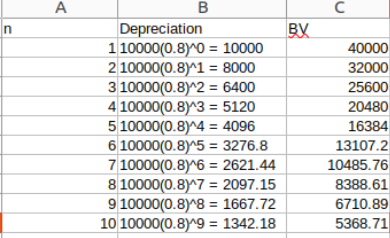
Q2:
Since O&M occurs every 5 years, we need to get an adjusted : every 5 years
The PW of the costs associated with this design (N = ) = 2500000 + (, 61.05%, ) 200000 = 2500000 + = 2827600.33
If the pool’s service is reduced to 40 years, then we have $200,000 annuity.
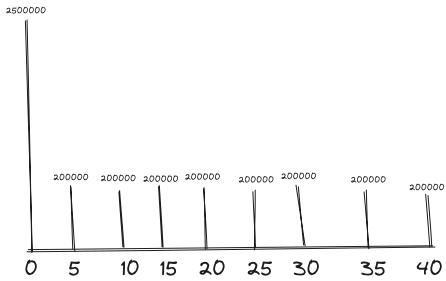
= 2500000 + (, 61.05%, 8) 200000 = 2820361.66
Q3:
a)
Given MARR = 8% yearly, the effective interest rate for O&M every 3 years is
every 3 years
So by BCR, this project is viable.
b) Modified BCR: O&M counts as one of the disbenefits.
So by modified BCR, this project is viable.
Q4:
a) Equating to equal repeated lives, we have LCD(4, 6) = 12
For the CR1000
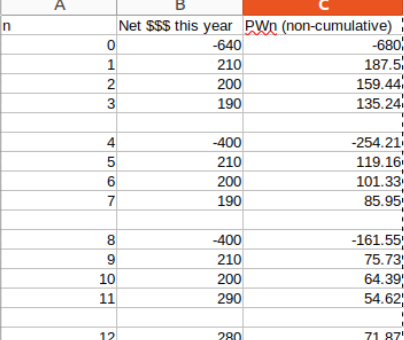
(At n = 12, we don’t need to re-purchase, we just have to scrap it)
Using AW, we don’t worry about repeated lives, so we just calculate with one lifecycle (N = 4):
For the CRX:

Again, at n=12, we only scrap it.
Using AW, we don’t worry about repeated lives, just calculate it using one lifecycle (n = 6)
Better to pick CRX with its MARR of 12%.
b) Find the salvage value where CR1000 is a better option.
So the CR1000 needs to have a salvage value of 816 or more to make it the superior option.
Q5:
Find the value of such that NPW = 0.
Via linear interpolation:
The IRR is roughly 23.99%. Since our IRR (23.99%) > MARR (14%), this is a viable project.
Q6:
a): Find the monthly payment sent to the bank
Monthly payment:
= $166530.75 \text{ monthly payment}b):
Q7:
a)
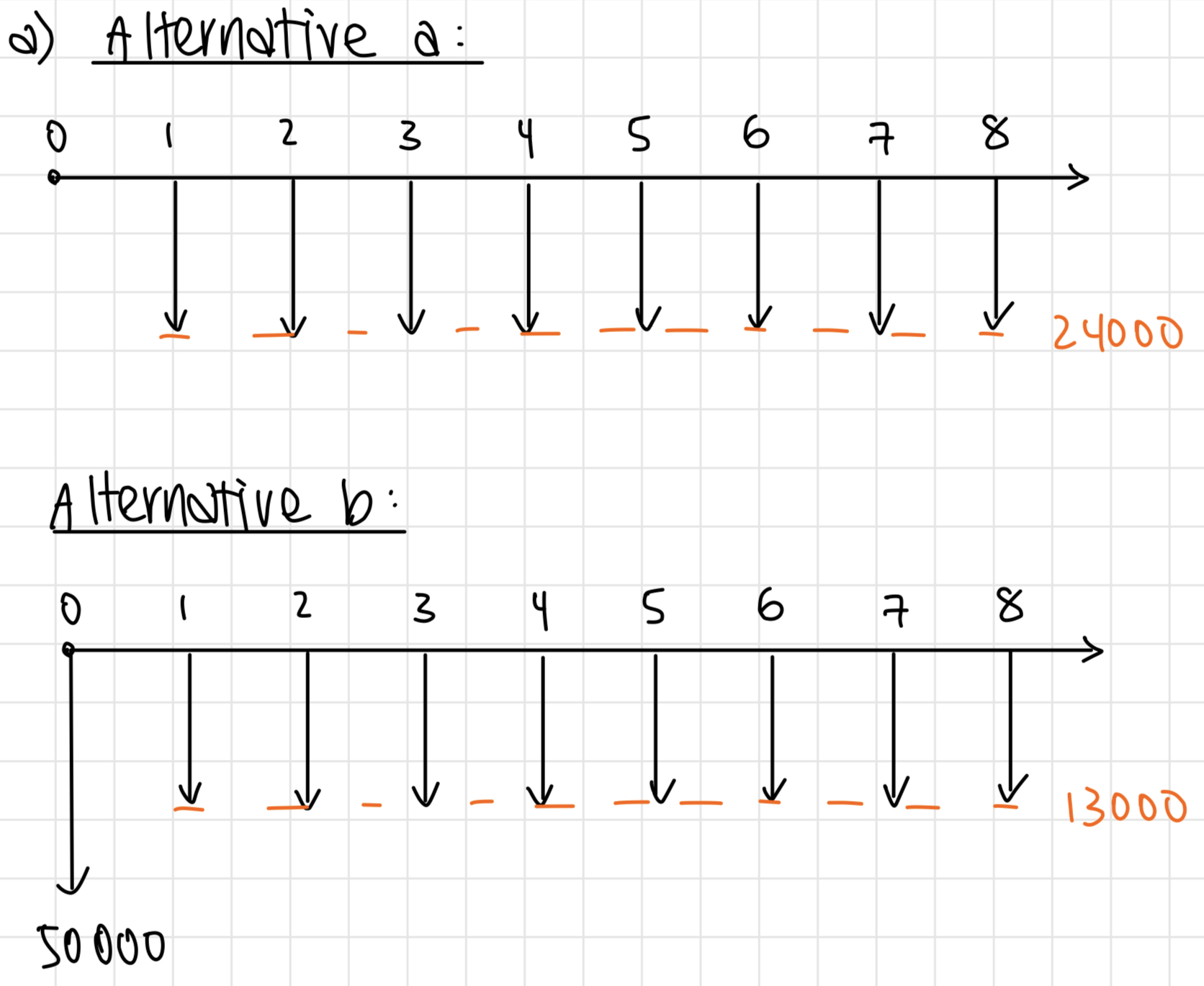
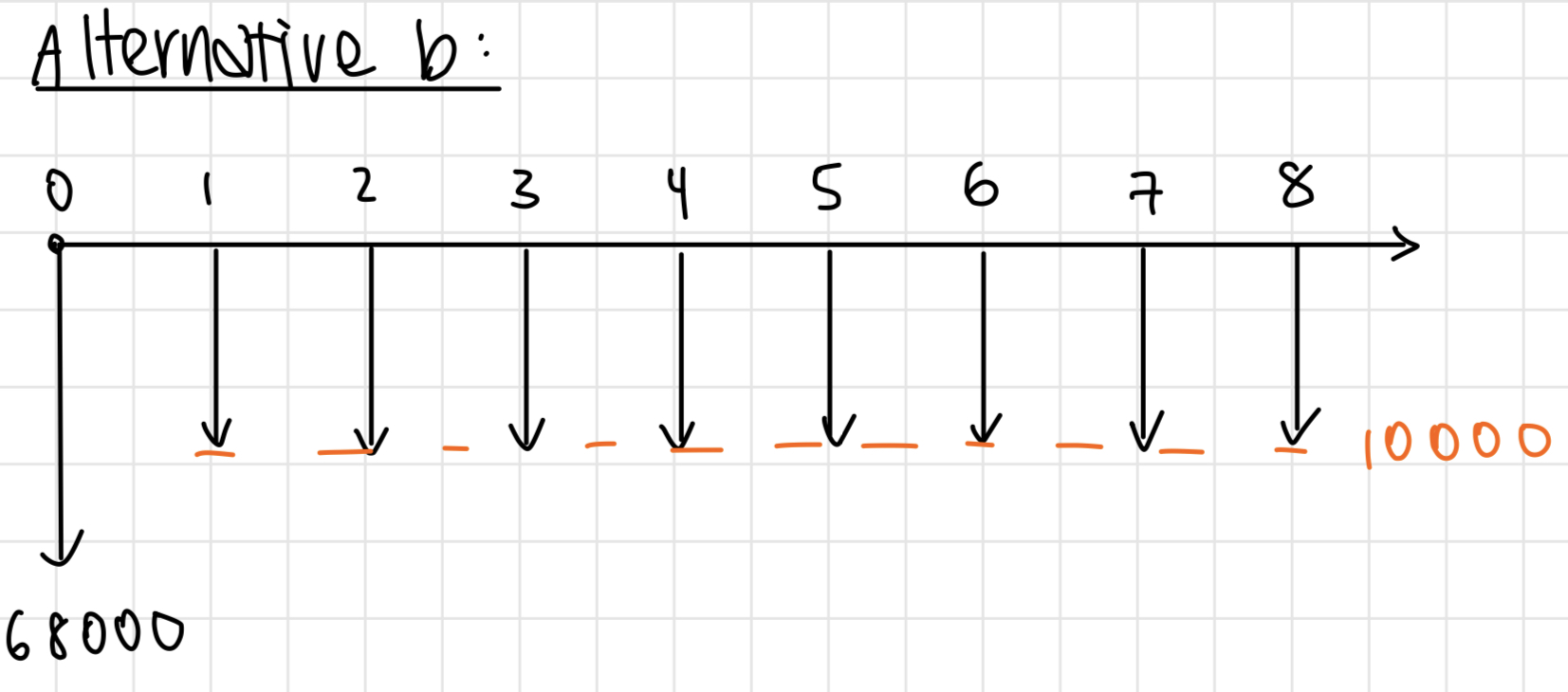
b)
Using interpolation, we get:
Between not doing anything and option B, we choose option B since it’s greater than the MARR and option B has a higher initial cost.
Using linear interpolation:
We choose option B between B and C. This is because we’re less than the MARR, and option B has a lower initial cost. So the best option is B, based on comparisons.
Q8:
a)
b) For a 10% increase in MARR:
c) Find the break-even (when PW = 0) If x is some number of hours:
Q9:
a) For the PV system:
For the wind system:
b) For this PV system: Initial cost O&M cost = $ Cash of the excess power4760$
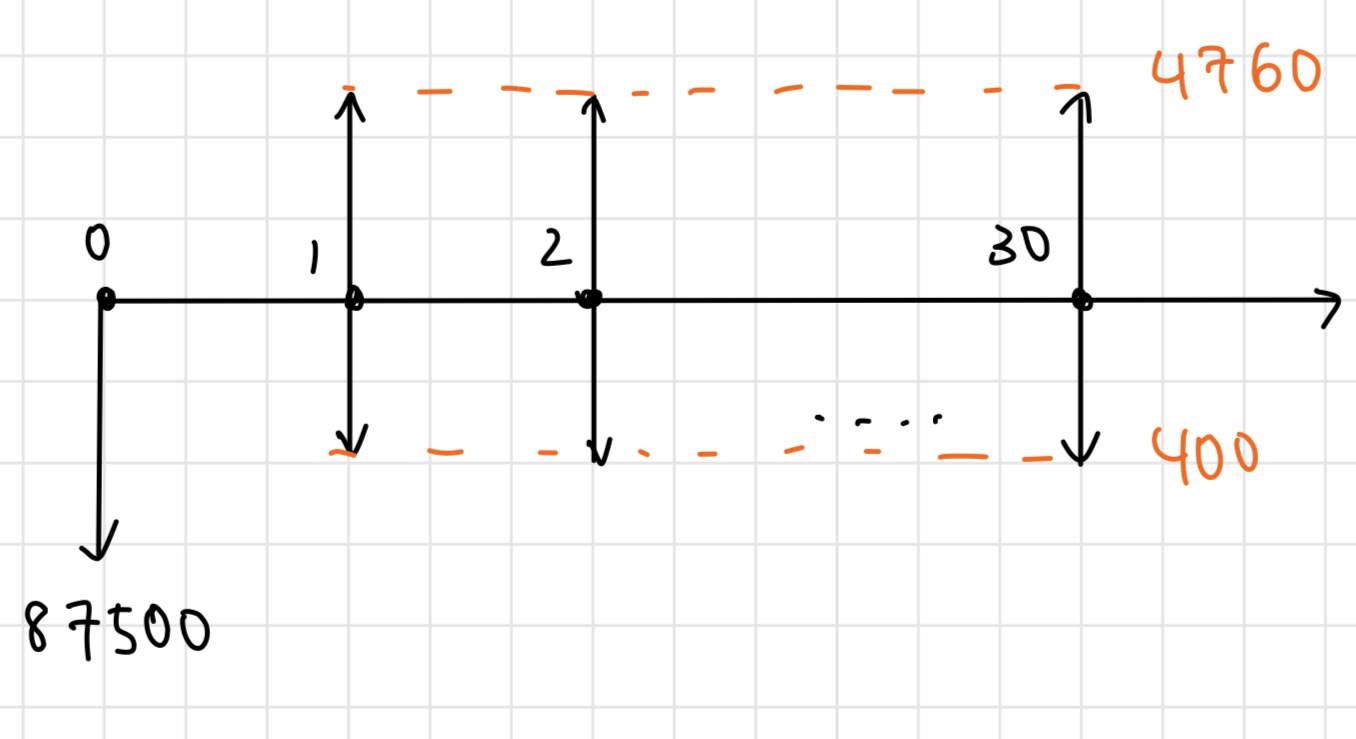
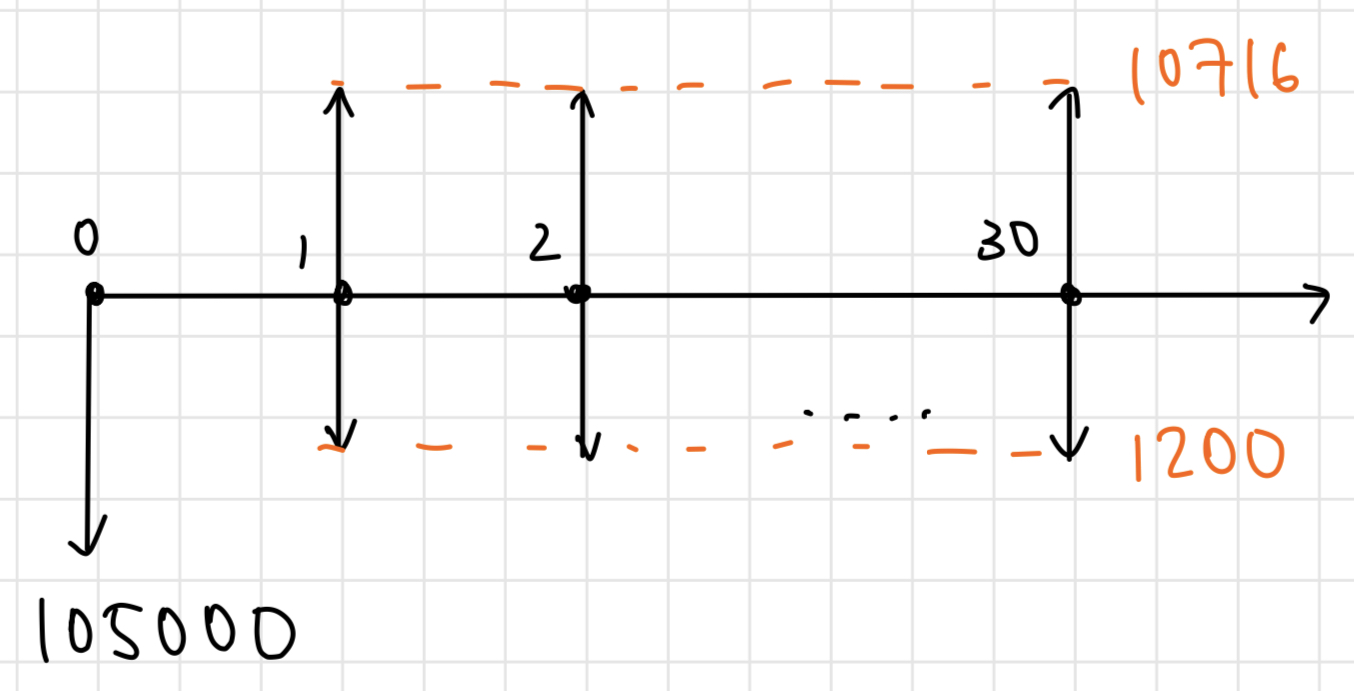
For the wind system: Initial cost = (35)(3000) = $105000
O&M cost = $\frac{1200}{year}$$
Cash of our excess power = (73.58 - 20)(1000)(.2) = $10716
c) For the PV system: Payback period = =
For the wind system: Payback period =
d) Since our projects are mutually exclusive, we’re allowed to use the method
Option 1: Do nothing Option 2: Install the PV system Option 3: Install the wind system
Cost of not doing anything = $
0 = -87500 - (400 - 5000)(, ^*, 30) + 4760(,i^*, 30) = -87500 + 9360
= 0.101 0.101 < 0.12, so we choose to do nothing.
0 = -105000 + (1200 - 5000)(, i^*, 30) + 10716(, i^*, 30) 0 = -105000 + 14516 = .135 .135 > .12
Thus, we choose option C.
Happy farm should choose to go with the wind system.
Q10
a) ![[IMG_323103D91974-1.jpeg|]]
b) EV 98000$
EV 93250$
EV = minimum of (EV and EV) = $93250
EV =
EV _4
EV = minimum of (, )
Since EV < EV, and < , we choose to test them, then to make a minor modification if our result is unfavourable.
c) From b), we know EV = and = 93250.