https://en.wikipedia.org/wiki/Radix_tree

Radix Trie / Compressed Trie

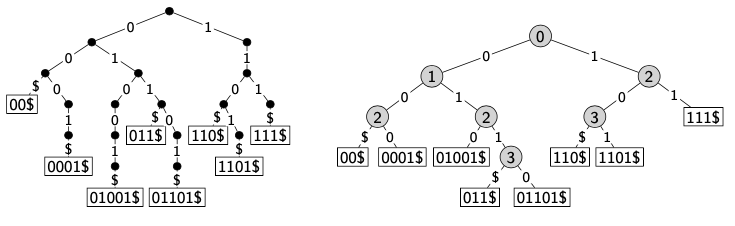
A variant of a Trie. Compress paths of nodes with only one child. Therefore the first at the root does not necessarily compare the first bit, since maybe it will be compressed for the first 3 bits when all the bit string stored starts with the same bits.

• Each node stores an index, corresponding to the depth in the uncompressed trie.
  • This gives the next bit to be tested during a search.
• A compressed trie with $n$ keys has at most $n-1$ internal nodes.

Practical Algorithm to retrieve information coded in Alphanumeric.

Compressed Tries: Search

• start from the root and the bit indicated at the node
• follow the link (line whatever) that corresponds to the current bit in $x$; return failure if the link is missing, that is there is no branch going down that matches with the bit in the string you are looking for.
• if we reach a leaf, explicitly check whether word stored at leaf is $x$
• else recurse on the new node and the next bit of $x$

Compressed Tries: Insert and Delete

• CompressedTrie::delete(x)
  • Perform search(x)
  • Remove the node $v$ that stored $x$
• CompressedTrie::insert(x)
  • Perform search(x)
  • Let $v$ be the node where the search ended
  • Conceptually simplest approach:
    • Uncompress path from root to $v$
    • Insert $x$ as in an uncompressed trie
    • Compress paths from root to $v$ and from root to $x$
  • But it can also be done by only adding those nodes that are needed

All Operations take $O(\left|x\right|)$ time.

Related

• Trie
• Multiway Trie