Final Value Theorem (FVT)

Theorem 3: Final Value Theorem

For a function $F(s)$, if

• is a proper rational function
• has the property that all the poles have real parts that are strictly negative with the exception of a single pole (of order 1)${}^a$ at $s=0$

or if $F(s)$ is the product of a function satisfying the above conditions multiplied by a complex exponential $e^{sT}$, then

${\lim }_{t\to \infty }f(t)={\lim }_{s\to 0}sF(s)$.

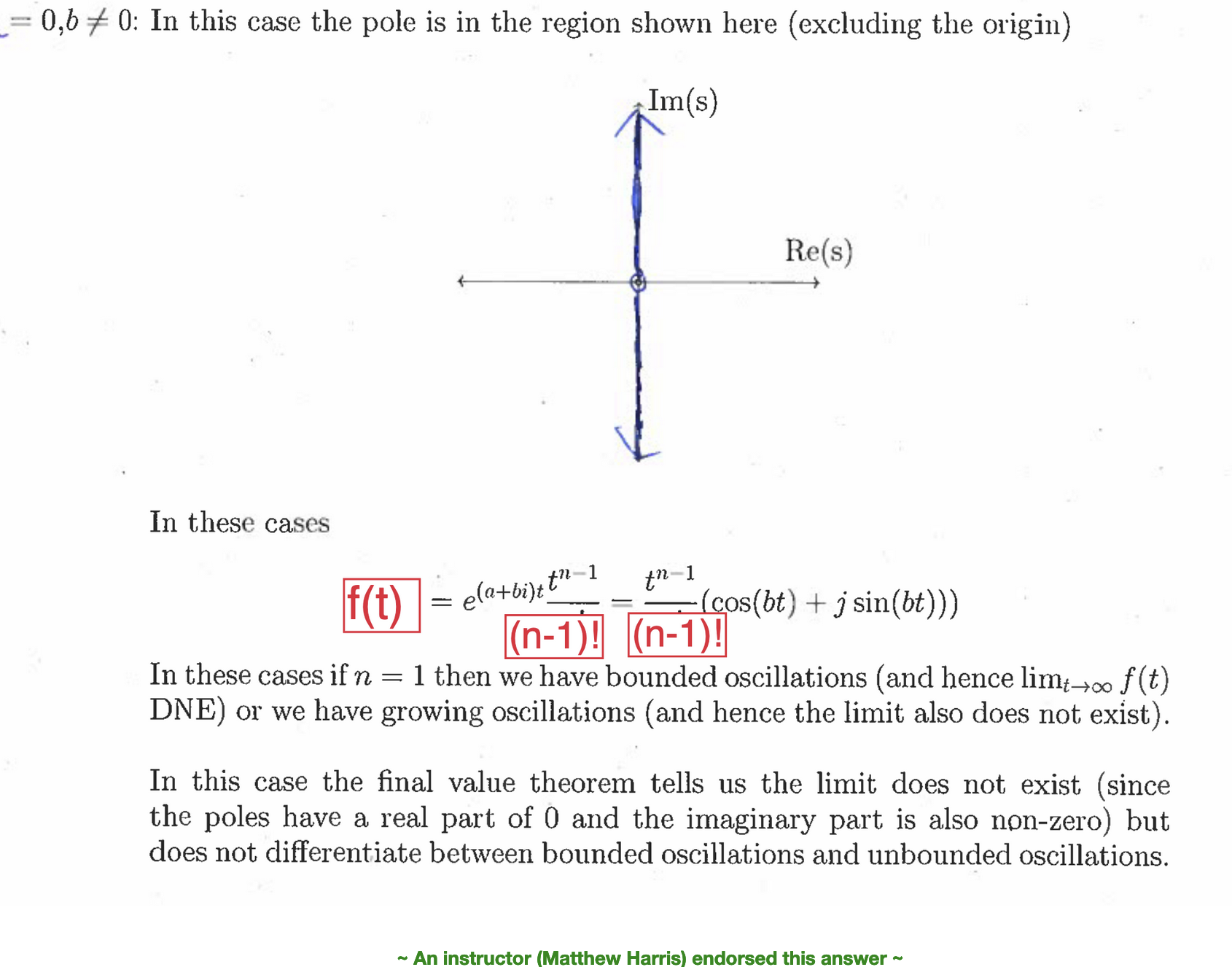
If the poles of a rational function do not satisfy the above condition, then ${\lim }_{t\to \infty }f(t)$ does not exist.

${}^a$i.e. $\frac{A}{s}$

Understanding this theorem:

• When it applies, the above gives us a way of computing the “final value” of $f(t)$ from $F(s)$ without computing the inverse Laplace transform and instead evaluating a limit in the complex plane.
• Again $s$ is generally complex so the limit is in the complex plane NOT the real number line. Limits at finite points in the complex plane are a bit different from infinite limits.
  • Here the formal definition of a limit of a complex valued function $F(z)$ at $x_{0\in }\mathbb{C}$ is the constant $L\in \mathbb{C}$ such that for every $ϵ\in {\mathbb{R}}^{+}$ there is a $\delta \in {\mathbb{R}}^{+}$ such that if $|z-z_0|<\delta$ then $|F(z)-L|<ϵ$ where $|\cdot |$ is the standard modulus function.
  • In practice for any problems of computing limits at 0, you can treat the limit as the standard limit you are used to working with.
• Connection to 2D limits from MATH119 - Calculus 2 for Enginering.
  • Provided that the limits exist, we have

$$\underset{s\to 0}{\lim }F(s)=\underset{(a,b)\to (0,0)}{\lim }Re(F(a+bj))+j\underset{(a,b)\to (0,0)}{\lim }Im(F)a+bj$$

Examples in notes.

Note

When the final value theorem does not apply, we do not know if the limit diverges or if it oscillates. Hence, we need more math to be able to ascertain if a solution is bounded or not (without computing the inverse transform)! See examples 8C and 8E for unstable systems and D for a stable but non-convergent system.

Questions

Lecture Example 6, From piazza question: FVT says that all the real parts should be strictly negative or there can be a pole at s=0 (not Re(s) = 0) of order 1. In the first part, the poles at + and - j have Re = 0, so that should give an undefined limit. What property/theorem are you using to be able to say the following for the ZIR:

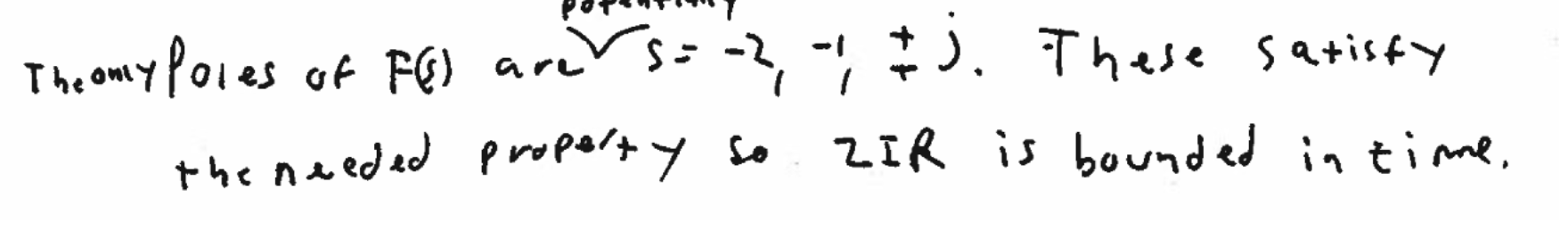
Even taking this as a truth makes the next part even more confusing.

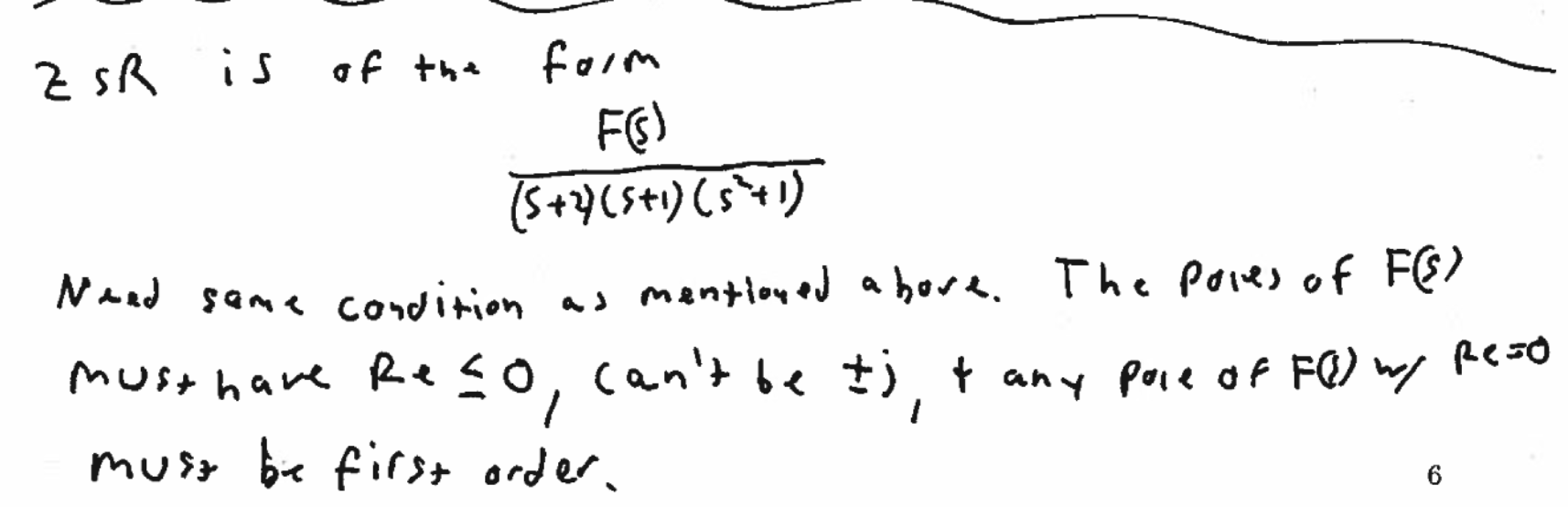
How does an extra pole at j or -j affect the boundedness here? Sure the order becomes 2, but there was already more than one pole anyways at Re(s) = 0. Unless the stated FVT is imprecise in that it should have been “there can be multiple poles at Re(s) as long as they are of order 1”.

I also understand that a limit not existing doesn’t mean that it isn’t bounded. If this is the case here, could you explain what theorem you used here to answer the question?

Ok Adrian figured it out.

As seen here, having Re(s) = 0 but Im(s) !=0 we are on the imaginary line. Here, we see that if n is 1, then it would just be cos(bt) + jsin(bt), which is bounded. If that isn’t the case, then we would have a growing t term, and thus it would be unbounded. This isn’t explicitly stated anywhere as a rule (so I’m hesitant to say this determinantly), but I think the professor refers to the phenomenon in a bunch of questions. Please correct me if I’m wrong.