Karp-Rabin Algorithm

From CS240

The idea: use hashing to eliminate some guesses.

• Compute fingerprint (hash function) for each guess!
• If different from $P$‘s fingerprint, then the guess cannot be an occurrence $\Rightarrow$ no need to do a string compare, that is continue..
• We use $mod$ $97$, since it’s rather rare for two strings to get the same hash result after modding it to 97, which is a big prime number, so if they do, then we have found a match, by calling $strcmp$.

Example:

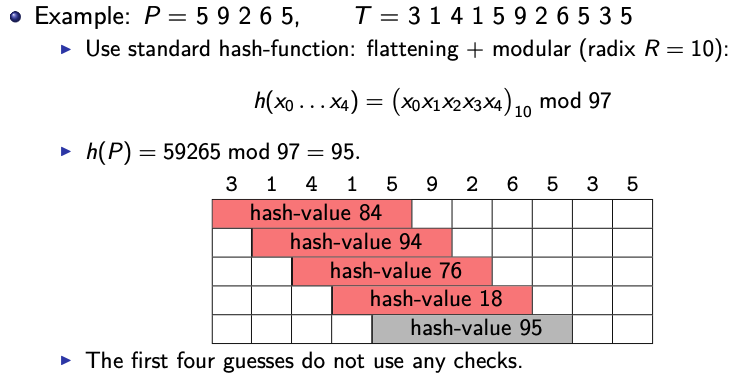
• Only compare when mod to the same number. Since comparing using $strcmp$ will take $\Theta (m)$.

First Attempt:

Notice, we compute the hash function of $P$ with mod $97$, then as in the example, we move forward by one and compute hash function of it with the length of $P$ and check. Until we finish going through $T$ or we found it. But notice, if the hash function doesn’t match, we don’t bother string comparing every time.

The running time is said to be $\Theta (mn)$ if $P$ not in $T$, but to be exact it is $\Theta (m(m-n))$. On piazza, they said that they kept $mn$ to simplify the function as much as possible.

The idea with using the fingerprint hashing, is that we can update the fingerprints in constant time!

• Since we use previous hash to compute the next hash
• $O(1)$ time per hash, except for the first one.

Example:

• Pre-compute 10000 mode 97 = 9
• Previous hash: 41592 mod 97 = 76
• Next hash: 15926 mod 97 = ?? To compute the next hash, we can observe that:

The whole idea: the first hash computation will take some time, but after that it is $O(m)$.

Questions

In the Karp-Rabin algorithm the hash value for each fingerprint of the text is always computed in constant time.

• False, the first computation is not constant time, but after the first, it will be.

In the Karp-Rabin algorithm, fingerprints can be updated in constant time only when the modulus $M$ is prime.

• False

All of them

Second