SE465

Object Relation Diagram (ORD)

Defining the ORD

• Class dependency information in Object Relation Diagram (ORD) can either come from reverse engineering or design documentation (e.g., UML)
• Straightforward for UML
  • Inheritance, composition, association in UML map directly to ORD
  • How should interface be handled?
• From source code?
  • Inheritance, interface?
    • Typically clear
  • Association or composition?
    • E.g., in Java, fields with type of other class
    • Lifecycle is linked for composition (may be tricky to determine with automatic garbage collection)

Prof's note

Composition is strong form of aggregation (where deleting whole deletes the parts too)

Difficult to determine in Java due to garbage collection

• From source code?
  • What about dependencies that are not expressed by inheritance, composition, or association?
  • E.g., a factory creates an object and returns it to the caller (Relationship of factory with class of the object is not inheritance, not composition, and not association – there is no field in the factory with the class as its type! However, the factory cannot be tested without the class.)
  • E.g., passing in an object as a parameter
  • E.g., creating an object in a method as a local variable
  • $\to$ Dependencies like that also need to be captured with an A edge in the ORD

Note

Look at the imports for clues!

Example Test Order

More in Integration Order…

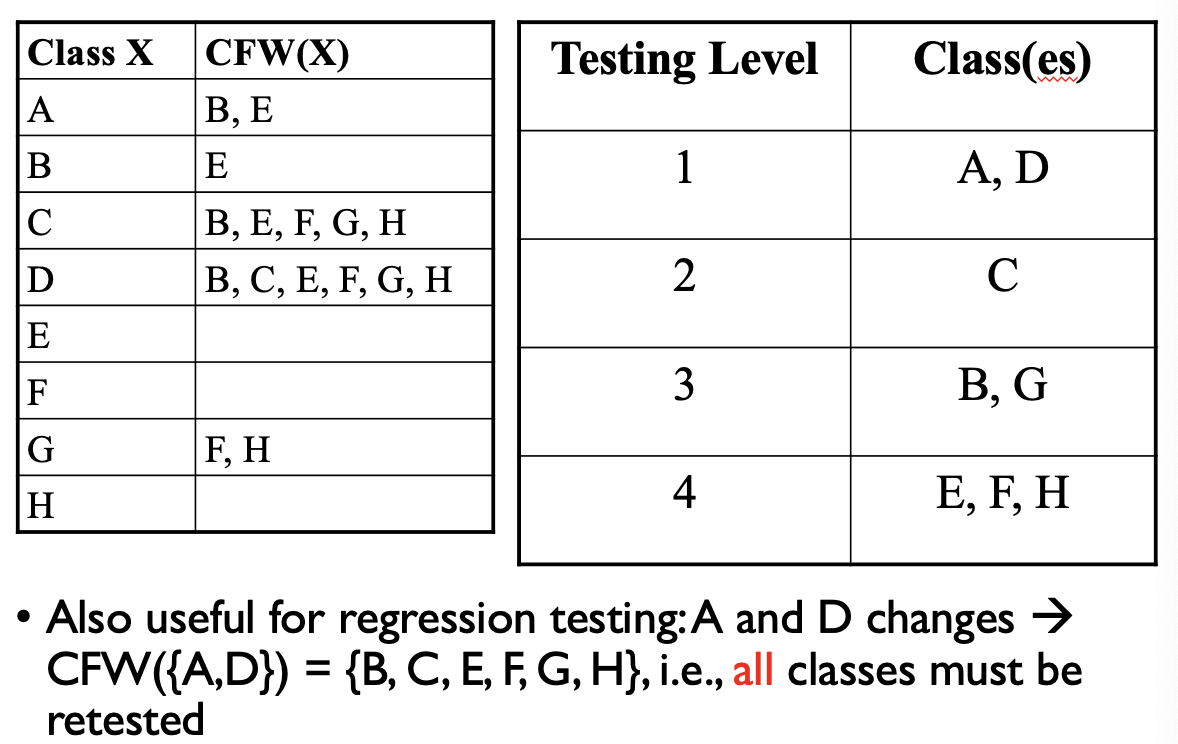
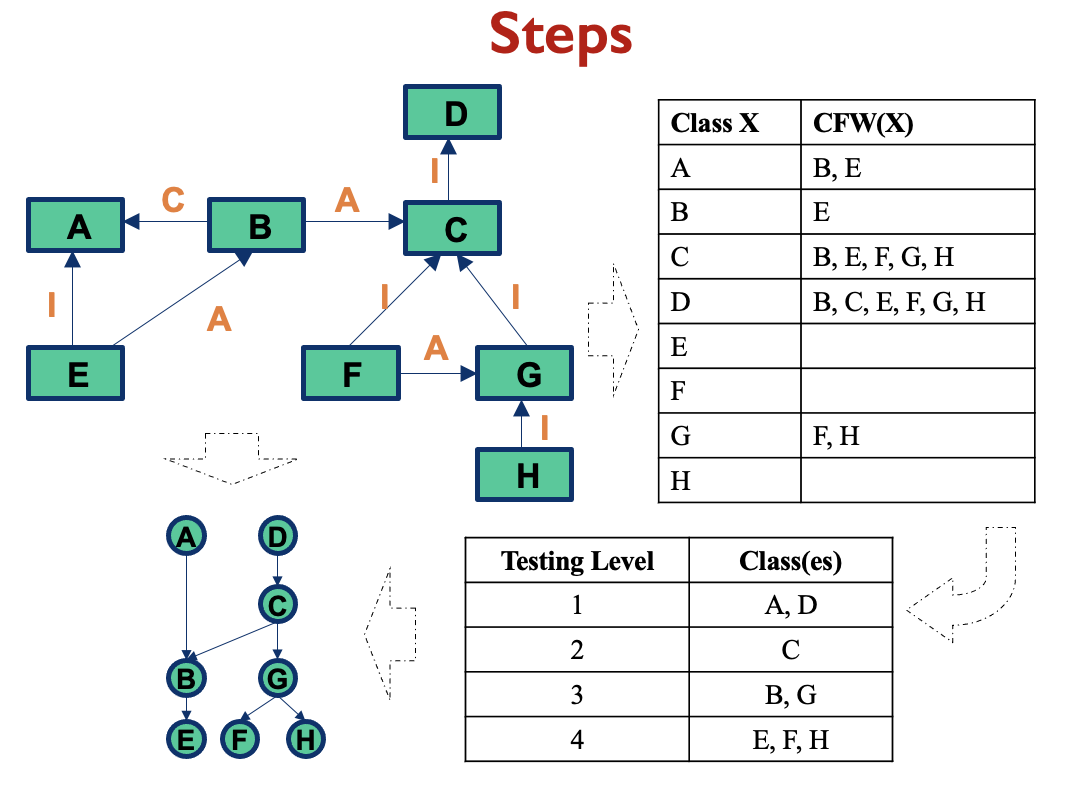
How to determine the Testing Level? I don't understand this step

When i did the example, I just went from bottom to top, so I started with E,F,H as the bottom level. Then I check the next classes that requires E,F,H and those would be a level up, and so on.

The Abstract Class examples are very hard to grasp

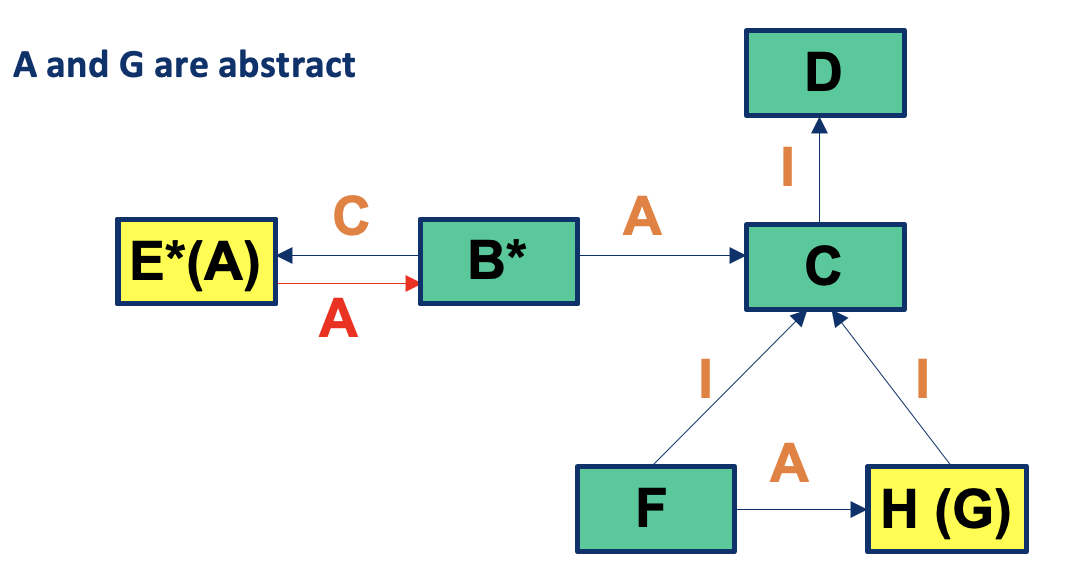
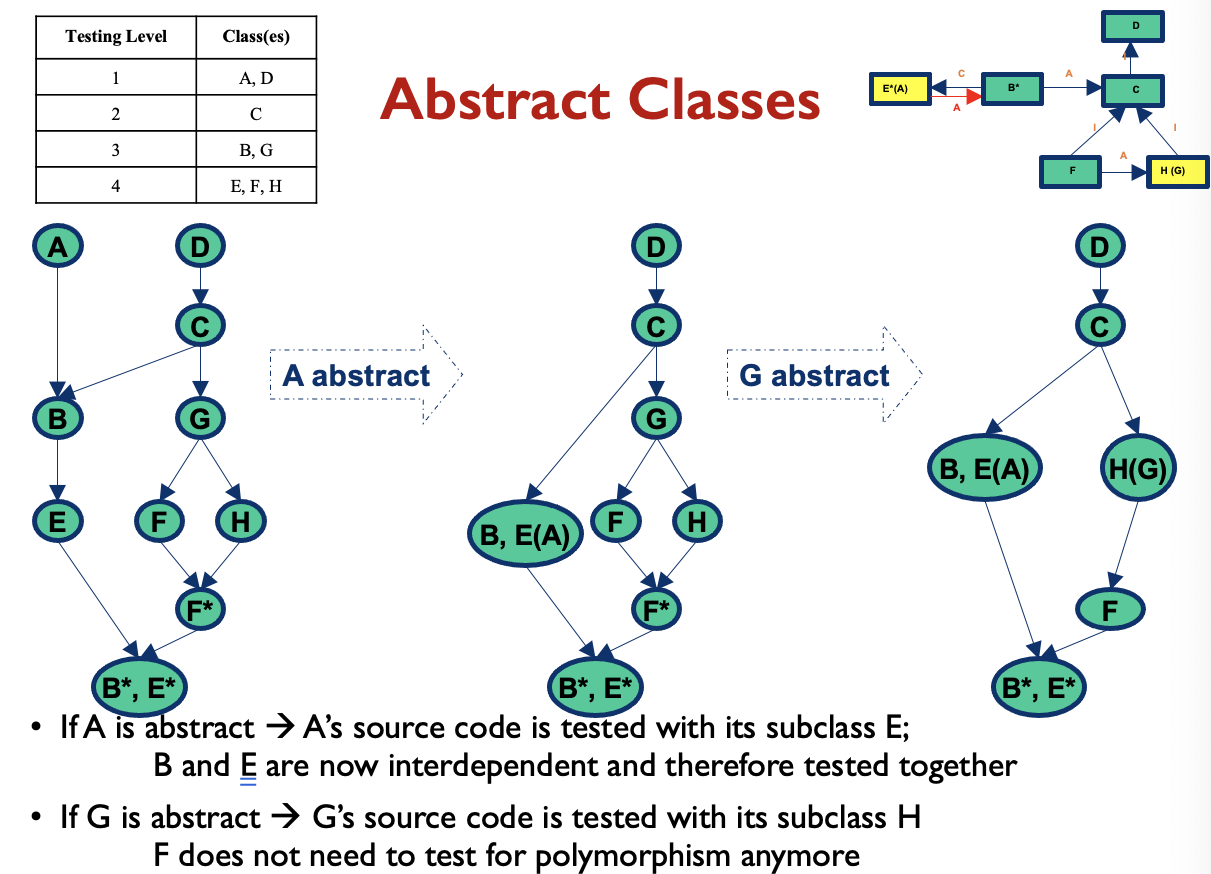
Abstract Classes

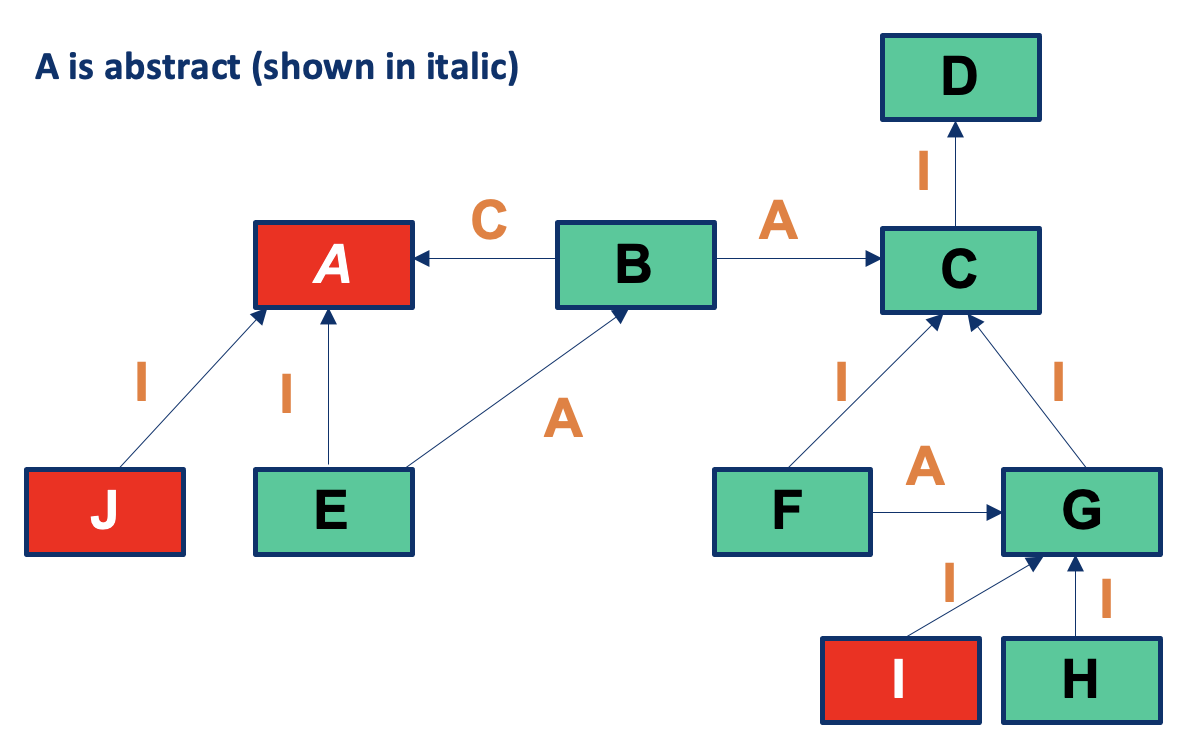
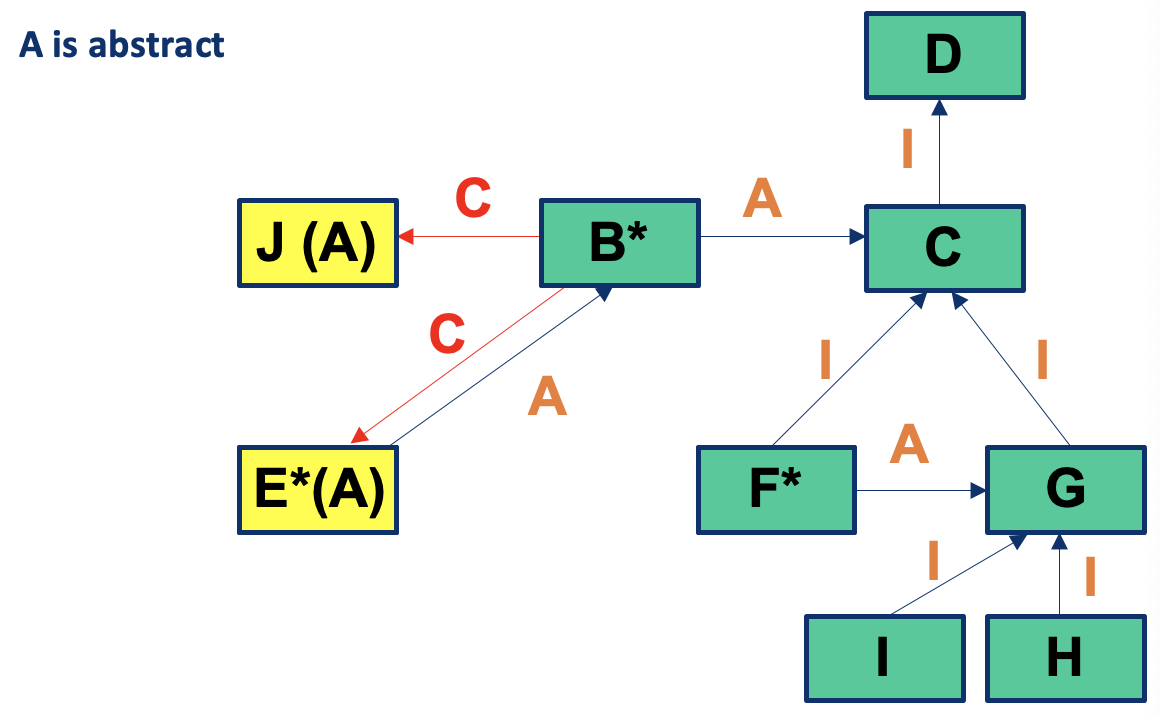
• Some testing levels become (partly) infeasible because of abstract classes (shown in italic)
  • If A is an abstract class, testing it at level 1 is unworkable
  • Testing B at level 3 now requires subclass E to be instantiated (instead of A)
  • E cannot be tested after B

• and same Testing level table as before (same example)

A and G are abstract:

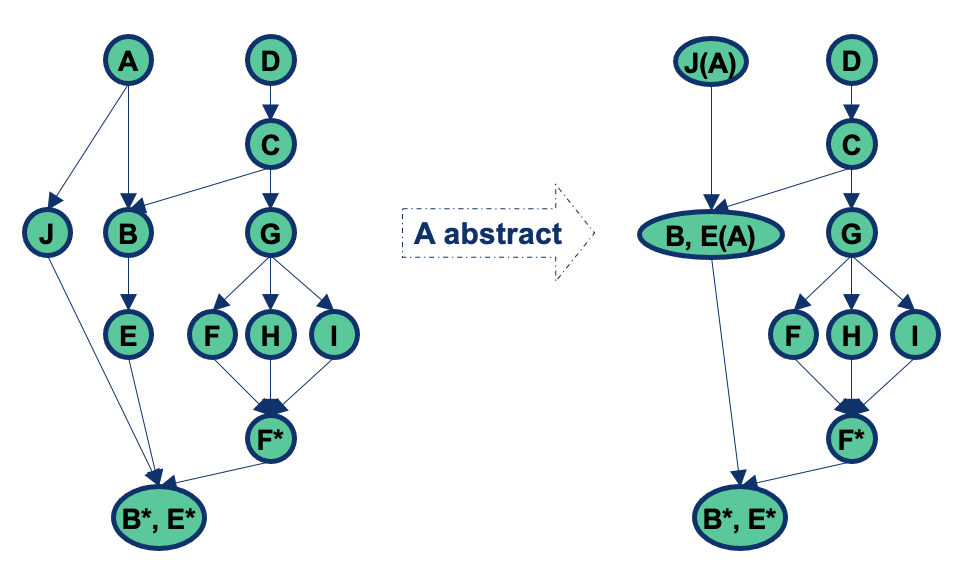
ORD Example (II)

A is abstract (shown in italic).

Integration Order (II) A is abstract