Proposititional logic Proof Theory Natural Deduction Semantic Tableaux

• Proving equivalence of formulas
• Logical laws
• Rules of thumb
• Relathionship between transformational proof and semantics
• Applications

Definition: Transformational proof ($\leftrightarrow$): a means of determining that two well-formed formulas of propositional logic, P and Q are logically equivalent by the (repeated) exhange of subformulas of P for logically equivalent subformulas that results in P being transformed into Q. Each step must follow a logical law.

Logical Laws

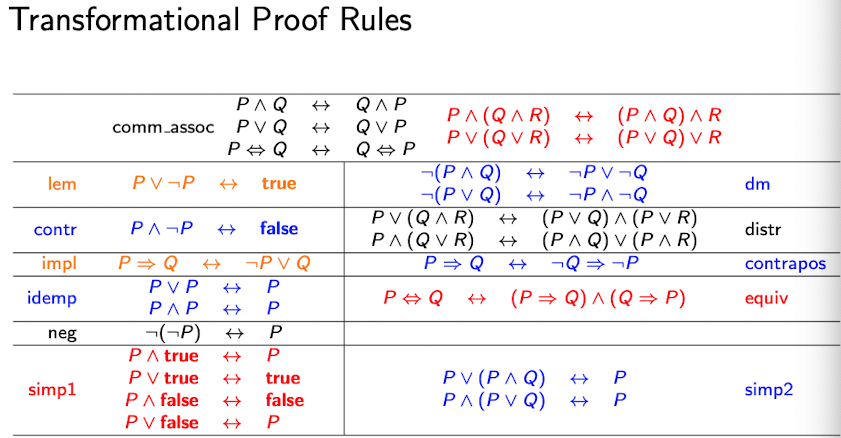
Rules of Thumb

1. Eliminate implication and equivalence using the law of implication, the law of equivalence and the contrapositive law backwards.
2. Simplify as soon as you can (simp1, simp2, idemp, neg, contr, lem).
3. Sometimes use the various kinds of simplification backwards to prepare for using distributivity.

Can use by MAGIC.

Transformational Proofs and Semantics

Transformational proof satisfies the following:

1. If P$\leftrightarrow$Q can be proved, then P$\equiv$Q (soundness of $\leftrightarrow$)
2. If P$\equiv$Q, then P$\leftrightarrow$ can be proved (completeness of $\leftrightarrow$)

Applications

Normal Forms

Every formula can be converted to an equvalent formula in CNF and DNF. The formulas consisting only of true or false are in both CNF and DNF.

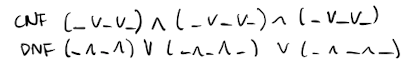
CNF

Definition: A formula is conjunctive nortmal form (CNF) if it is a conjunction of one or more clauses, where a clause is a disjunction of literals or a single literal.

To see if a formula is not valid (not a tautology) in CNF, find one clause that does not have contradictory literals and it is not valid.

DNF

Definition: A formula is in disjunctive normal form (DNF) if it is a disjunction of one or more clauses, where a clause is a conjunction of literals or a single literal