Range Searching

So far, we have $search(k)$ looks for one specific item.

New operation $RangeSearch$: look for all items that fall within a given range.

• Input: A range, i.e. an interval $l=(x,x^{\prime })$
  • May be open or closed at the ends
• Want: Report all KVPs in the dictionary whose key $k$ satisfies $k\in l$

• Let $s$ be the output-size, i.e. the number of items in the range

Note

Sometimes $s=0$ and sometimes $s=n$; we therefore keep it as a separate parameter when analyzing the run-time.

Range searches in existing dictionary realizations

Unsorted array: Range search requires $\Omega (n)$ time: We have to check for each item explicitly whether it is in the range.

Sorted array: Range search on A can be done in $O(\log n+s)$:

BST: Range searches can similarly be done in time $O(height+s)$ time. Will see this later in detail? In BST range search, there are always $\Theta (\log n)$ distinct nodes?

Multi-Dimensional Range Search

(Orthogonal) d-dimensional range search: Given a query rectangle $A$, find all points that lie within $A$.

The time for range searches depends on how the points are stored.

• We can store the points in a 1-dimensional dictionary $\to$ Problem: range search on one aspect is not straightforward??
• We can use one dictionary for each aspect $\to$ Problem inefficient, waste of space

Better idea: Design new data structures specifically for points.

• Quadtree
• kd-Tree
• Range Tree

Definition of aspect: each item has d aspects (coordinates): $x_0,x_1,...,x_{d-1}$. Aspect values ($x_i$) are numbers. Each item corresponds to a point in d-dimensional space. Concentrate on $d=2$.

Range search Data Structures summary

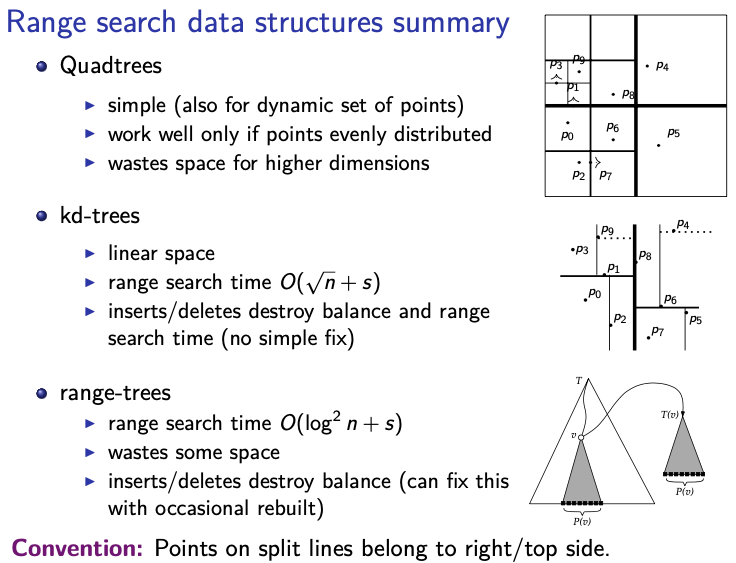
Questions

In BST range search, there are always $\Theta (\log n)$ distinct nodes.

• False, why?

The best-case runtime of a 1-dimensional range search on a balanced binary search tree with $n$ nodes is:

• $\Theta (\log n)$???? What about the worst-case: $\Theta (n)$? I don’t remember why?