Skip List

The motivation of skip lists to imitate binary search in an ordered Linked List. To do binary search on a linked list!

In my opinion, SkipList was introduced as it is one possible implementation of dictionary ADT and it has interesting runtime as well.

With an ordered array, we can directly do binary search, but we cannot do binary search directly on a linked list

A hierarchy $S$ of ordered linked lists (levels) $S_0,S_1,...,S_h$:

• Each list $S_i$ contains the special keys $-\infty$ and $+\infty$ (sentinels)
• List $S_0$ contains the KVPs of $S$ in non-decreasing order. (The other lists store only keys, or links to nodes in $S_0$)
• Each list is a subsequence of the previous one
• List $S_h$ contains only the sentinels; the left sentinel is the root

• Each KVP belongs to a tower of nodes
• There are (usually) more nodes than keys
• The skip list consists of a reference to the topmost left node
• Each node $p$ has references $p.after$ and $p.below$

Search

• We will need a function called $Predecessor$ which will return a stack with all the predecessor of $k$ on each level.
  • This function will be useful for insert/delete.

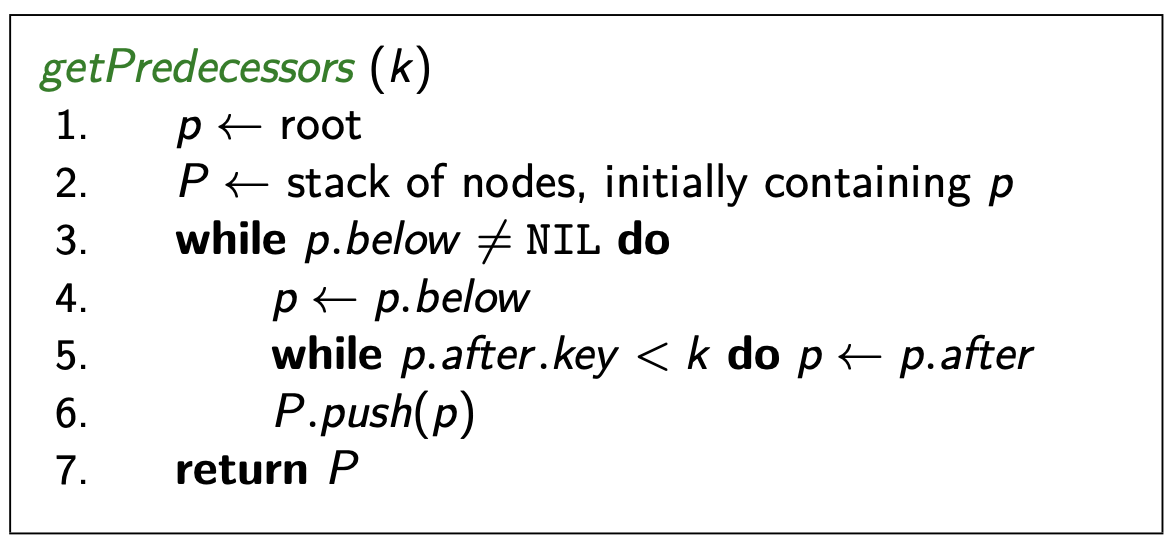Returns a stack of the predecessor of $k$ on each level.

Pseudocode for search: Top of the stack is the bottom row of the skip list.

We check what is right after the top of the stack, if we find $k$ then we’ve found it. If not, then $k$ is not in the list.

Search is $O(\log n)$ $\to$ logarithmic since we don’t do much steps in each level. (Expected time that is)

Insert

• We randomize the construction of the skip list by randomly repeatedly tossing a coin until we get tails.
• Let $i$ the number of times the coin came up heads, $i$ is the height of the key to be inserted. If there is one element, the height is 0, if two elements, the height is 1, and so on.
• Increase height $h$ of skip list, if needed to have $h>i$ levels.
• Use $getPredecessors(k)$ to get stack $P$.

Deletion

It is easy to remove a key since we can find all predecessors.
Then eliminate layers if there are multiple ones with only sentinels.

Analysis of Skip List

Expected space usage: $O(n)$ Expected height: $O(\log n)$

In big $O-notation$

• Search: $O(\log n)$ average time
  • number of drop-downs = height
  • expected # forward-steps is $\le 1$ in each level
  • expected total # forward-steps is in $O(\log n)$
• Insert: $O(\log n)$ expected time (and average runtime?? I assume)
• Delete: $O(\log n)$ expected time

What is the average-runtime? Is it $O(\log n)$? Yes. Whats the worst-case runtime for every operations? $O(n)$?

worst-case Skip List

If the height is bounded by $h$, then the worst case is $O(n+h)$, however if it is unbounded, then the worst case is $\infty$.

Summary: $O(n)$ expected space, all operations take $O(\log n)$ expected time!

Reordering

Recall: Unordered list/array implementation of ADT Dictionary search: Θ(n), insert: Θ(1), delete: Θ(1) (after a search)

Questions

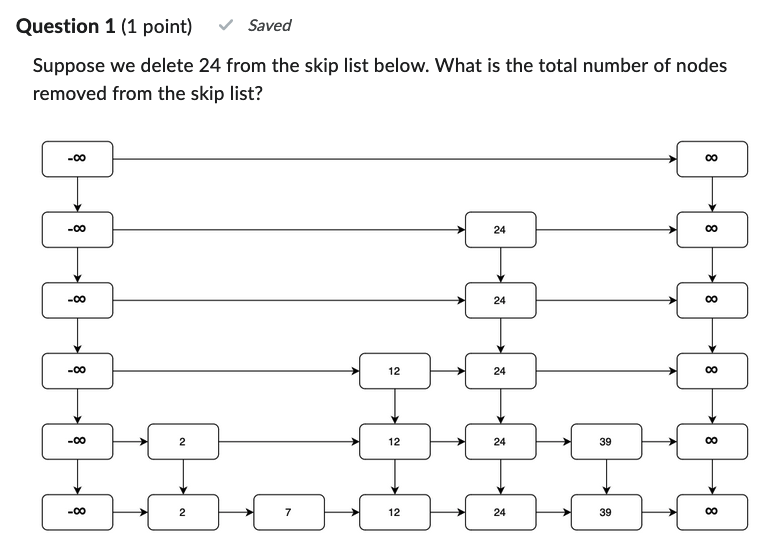
• 9, since we remove all five 24 nodes, and since we have two extra towers, we will also need to remove 4 sentinels? $5+4=9$ nodes. It is 9.
• So in delete, we adjust the height of the whole skip list. Yes. The height of the skip list the the max height of the towers, so from left to right we have tower height: 2, 1, 3, 2 after deletion. So, our skip list need to adjust its height to 3. (Start counting from bottom by 0).

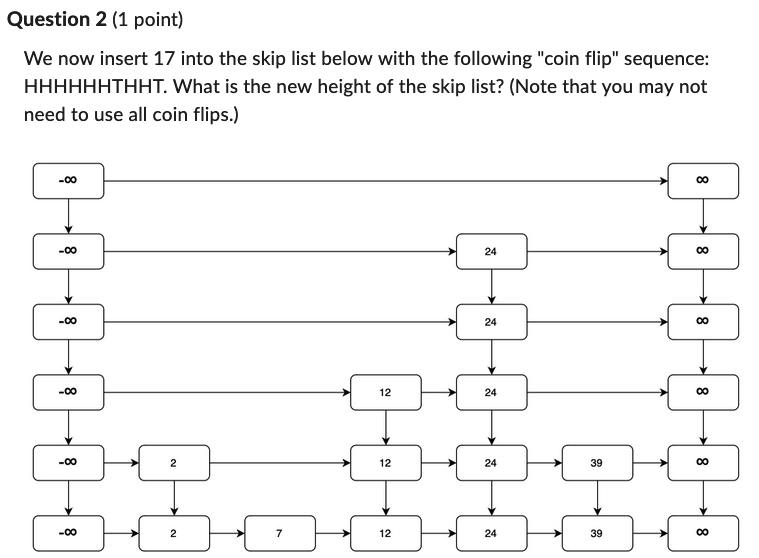
• We use the H before the T, so that is $6H$, a tower of height $i=6$ for the 17 node.
• My question is, do we count from the bottom starting from 0 or 1? In my understanding, looking at the picture, 24 is a tower of $i=5$.
• So our skip list will have a height of $6+1=7$. It would be 7 in the same convention used in @928, because you would unconditionally insert in S0 before the first flip, so you should end up with a node on S6 after insertion.

• $[-\infty ,-\infty ,-\infty ,12,12,12]$

In a skip list with $n$ items where the tower has been bounded by a constant $c=100$, the worst-case runtime for search is $\Theta (n)$.

• The skip list guarantees a runtime of $\Theta (\log n)$ for all operations? So false?
• NO, the answer is True. But why? (ask on piazza)

Running $Search(k)$ in a skip list may not take the shortest path to reach the node in $S_0$ with key $k$.

• node in $S_0$ means the last row in the skip list, and node with key $k$, is the only node on that row that we are looking for.
• True, it may take longer paths through higher levels, bypassing some nodes in the base level?

In a skip list with $n$ elements and of expected height, what is the best-case runtime of search?

• $\Theta (\log n)$

What is the probability that a tower in a ski plist has exactly 3 nodes?

• $\frac{1}{2}\times \frac{1}{2}\times \frac{1}{2}=\frac{1}{8}$

What is the probability that a tower in a skip list has at least 3 nodes?

• $\frac{1}{4}$, why??

Suppose we query $41,62,23,41$ in that order in the array below.

$$[8,41,53,37,62,23,12]$$

What is the final array after these queries, supposing that we use the Transpose Heuristic and how many comparisons are made in total.

• 14 comparisons, Array: $[41,8,53,62,23,37,12]$

Suppose we have the same array and queries as in the previous question. What is the final array and the number of comparisons made after using the MTF heuristic?

• 16 comparisons, Array: $[41,23,62,8,53,37,12]$

You are given a dictionary $D$ implemented using the Transpose heuristic, with $n$ keys, stored as an unordered linked list $L$. Suppose you want to perform a sequence of $k$ searches on keys present in $D$ where the number of different keys searched for is a constant $c$ and $c\le k$. The worst-case runtime to perform all $k$ searches is:

• $\Theta (k+n)$? no, it’s $\Theta (kn)$
• Since it’s $k$ items we are looking for and accessing in dictionary is $\Theta (1)$, then a place in the dictionary can have a linked list that is $n$ long. How does Transpose heuristic play a role in this?
• In the case with Transpose, you can search for nth key and n-1th key alternating (i.e. nth, n-1th, nth, n-1th…).
• However, in the worst case, the desired item might always be at the end of the list, resulting in a linear search time of O(n) for each of the k searches. Therefore, the worst-case runtime for performing all k searches is $\Theta (kn)$.

You are given a dictionary $D$ implemented using the MTF heuristic, with $n$ keys, stored as an unordered linked list $L$. Suppose you want to perform a sequence of $k$ searches on keys present in $D$ where the number of different keys searched for is a constant $c$ and $c\le k$. The worst-case runtime to perform all $k$ searches is:

• How does MTF heuristic play a role in this??
• $\Theta (kn)$, in the case with MTF, worst-case would be when you search in reverse order and repeat it if $k\ge n$.

Give a linked list of $n$ items implemented with the MTF heuristic, what is the fewest number of searches to cause the first item to be relocated to the end of the list?

• Need $n-1$ searches to cause the first item to be at the back

Given a linked list of $n$ items implemented with the Transpose heuristic, what is the fewest number of searches to cause the first item to be relocated to the end of the list?

• n-1