N-Thread Mutual Exclusion

Now, we increase the mutual exclusion game’s difficulty/complexity by increasing the number of players from 2 to $N$.

Prioritized Retract Intent

Figure 6.12 shows a structured version of the B-L algorithm:

• The algorithm has an array of bytes (only one bit is used!), one per thread, to represent the $N$ blackboards needed on the bathroom door.
• This array is passed to each thread along with the size of the array and a position/priority value.
• Low subscript values have higher priority
• Entry protocol has 2 steps:
• sets its own intent, and then linearly search in the high-priority to see if a higher priority has declared intent. If found, searching thread retracts its intent and busy waits until the higher priority thread retracts its intent, and then searching thread begins the search over again from its starting position as in:
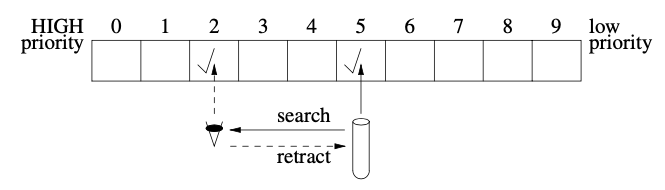
• only after a thread has searched all the way up the high priority direction and found no thread with higher priority intent, then moves to second step
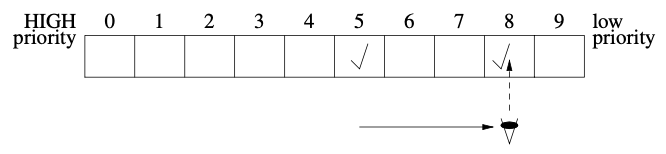
  • second step: a thread searches in the low-priority, searching thread never retracts its intent; just busy waits until low-priority thread retracts its intent either by leaving the CS or retracting its intent in the entry protocol and continues along the list:
• When a thread reaches the end of the list, it sees no lower priority thread in the critical section and so it can safely enter it.

In essence, the lower priority thread started searching before the higher priority thread, and now, the higher priority thread waits for it to complete.

When the lower priority thread finds a high- priority thread’s intent, it retracts its intent.

High priority thread DOES NOT retract its intent when performing the lower priority search.

B–L is RW-safe requiring no underlying atomicity!

Tournament

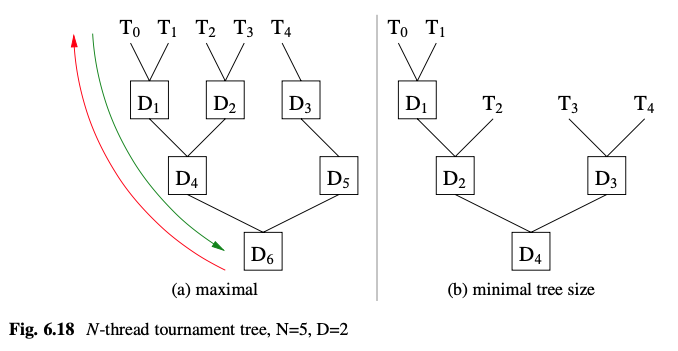
To simplify N-thread solutions and reduce amount of scanning. A tournament uses Divide-and-Conquer, where only one of every D threads progresses to the next round, and others busy wait.

For all trees, threads start at the leaves of the tree, and ${\log }_2(N)$ Ne levels of internal nodes are needed to implement the tournament.

Each node is a 2-thread solution for mutual exclusion, such as Dekker, Kessels or Peterson. Each thread is assigned to a particular leaf where it begins the mutual exclusion process.

At each node, the 2-thread algorithm ensures an arriving thread is guaranteed to make progress (rule 5); i.e., the loser at each node eventually becomes the winner and continues to the next level.

Therefore, each thread eventually reaches the root of the tree and enters the critical section.

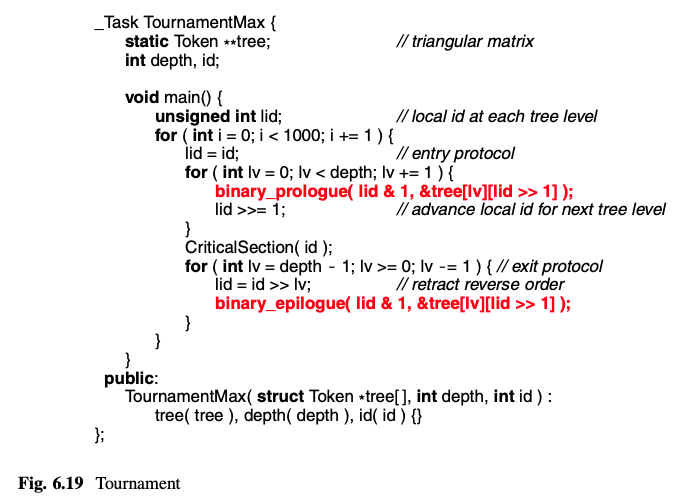
• Fig. 6.19 shows the basic code for any tournament algorithm.
• No starvation because each node guarantees progress, so each thread eventually reaches the root.
• Tournament algorithm RW-safety depends on MX algorithm; tree traversal is local to each thread.
• Tournament algorithms have unbounded overtaking as no synchronization among the nodes of the tree.
• • For a minimal binary tree, the tournament approach uses (N − 1)M bits, where (N − 1) is the number of tree nodes and M is the node size (e.g., intent, turn).

Arbiter

Full-time arbitrator thread to control entry to the critical section: