Breadth-First Search

Seen in CS341.

As long as the queue is not empty based on the order of queue. Take things out. and look at all the neighbours. If the neighbours is not visited, we enqueue it.

Time Complexity

Analysis:

• each vertex is enqueued at most once
• so each vertex is dequeued at least once
• so each adjacency list is read at most once (since we visit all the neighbours of a vertex only if it has not been visited)

For all $v$, write $d_v=$ number of neighbours of $v=$ length of $A[v]=$ degree of $v$.

$$O(\sum _v{d}_{v)}=O(m)$$

cf. the adjacency array $A$ has $2m$ cells (Handshaking Lemma)

Total: $O(n+m)$

Analysis: Before proving the various properties of breadth-first search, let’s take on the easier job of analyzing its running time on an input graph . We use aggregate analysis, as we saw in Section 16.1. After initialization, breadth-first search never whitens a vertex, and thus the test in line 13 ensures that each vertex is enqueued at most once, and hence dequeued at most once. The operations of enqueuing and dequeuing take $O(1)$ time, and so the total time devoted to queue operations is z$O(V)$. Because the procedure scans the adjacency list of each vertex only when the vertex is dequeued, it scans each adjacency list at most once. Since the sum of the lengths of all adjacency lists is $|V|$, the total time spent in scanning adjacency lists is $O(V+E)$. The overhead for initialization is $O(V)$, and thus the total running time of the BFS procedure is $O(V+E)$. Thus, breadth-first search runs in time linear in the size of the adjacency-list representation of $G$.

Correctness

Claim

For all vertices $v$, if $visited[v]$ is true at the end, there is a path $s⇝v$ in G.

to-understand Proof. Let $s=v_{0,}...,v_k$ be the vertices fort which visited is set to true, in this order. We prove: for all $i$, there is a path $s⇝v_i$ by induction.

• OK for $i=0$
• suppose true for $v_{0,}...,v_{i-1}$. when $visited[v_i]$ is set to true, we are examining the neighbours of a certain $v_j$, $j<i$. by assumption, there is a path $s⇝v_j$ because {$v_{j,}{v}_i$} is in $E$, there is a path $s⇝v_i$
• $visited[v_0]$ is true
• if $visited[v_i]$ is true, we will examine all neighbours $u$ of $v_i$ so at the end of Step 7, all $visited[u]$ will be true, for $u$ neighbour of $v_i$. In particular, $visited[v_{i+1}]$ will be true

Lemma

For all vertices $v$, there is a path $s⇝v$ in $G$ if and only if $visited[v]$ is true at the end.

Applications

• testing if there is a path $s⇝v$
• testing if $G$ is connected in $O(n+m)$

Exercise

For a connected graph, $m\ge n-1$.

Thu Jan 25, 2024

I visit some node $v$, but why do we do that in BFS?

If I have a parent array, do we still need a visited array?

• No, we can just go check the parent array and check if it’s null or it visited the child.

In the textbook, they use predecessor to mean parent. It’s more general. I kinda got used to it.

$\to$ Based on this algorithm, we can form a tree!

$Level[v]$ is the parent.

Example for the algorithm (i’ve recorded the whole process):

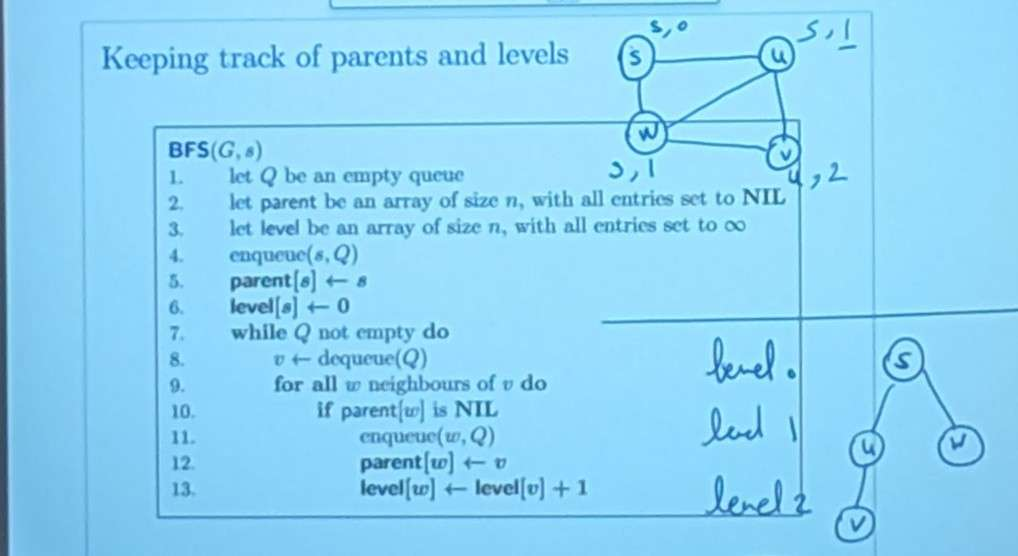
BFS Tree

BFS Tree

the BFS Tree $T$ is the subgraph made of

• all $w$ such that $parent[w]\ne NIL$
• all edges $w,parent[w]$, for $w$ as above (except $w=s$)

Claim

The BFS tree $T$ is a tree.

Proof: by induction on the vertices for which $parent[v]$ is not NIL.

• when we set $parent[s]\leftarrow v$, only one vertex, no edge.
• suppose true before we set $parent[w]\leftarrow v$ $v$ was in $T$ before, $w$ was not, so we add one vertex $w$ and one edge $v,w$ to $T$, so $T$ remains a tree.

Remark: we make it a rooted tree by choosing $s$ as a root.

Shortest paths from the BFS tree

Sub-claim 1

The levels in the queue are non-decreasing

Proof: Exercise

Sub-claim 2

For all vertices $u,v$ if there is an edge $u,v$, then $level[v]\le level[u]+1$.

…

I’m very confused: I have recordings.

Very important claim:

Claim

For all $v$ in $G$:

• there is a path $S\to v$ in $G$ iff there is a path $s->v$ in $T$
• if so, the path in $Tisashortestpathand$level[v]=dist(s,v)$

• $level[v]\le level[u]+1$

todo complete the notes, I did it in cs341 but forgot to update over here.