Depth-First Search (DFS)

Learned in CS341.

A depth-first search algorithm exhausts each one direction before trying another direction.

DFS implementations are based on stacks, either implicitly (recursion) or explicitly (as with queues for BFS).

In DFS, the frontier is managed as a Stack data structure.

• Pros:
  • At best, this algorithm is the fastest. If it “lucks out” and always chooses the right path to the solution (by chance), then depth-first search takes the least possible time to get to a solution.
• Cons:
  • It is possible that the found solution is not optimal.
  • At worst, this algorithm will explore every possible path before finding the solution, thus taking the longest possible time before reaching the solution.

Notice that visited is outside the for loop

This is my intuition. You mark the node as visited while you are inside the DFS function. And then process it. This is NOT the case with BFS , which you mark it inside the for loop. Then, process it a bit later. That is because they use a Queue data structure.

In CS341, they put it in the loop, guess it’s fine too.

DFS Tree

Unlike the BFS, whose predecessor subgraph forms a tree, the predecessor subgraph produced by a DFS may be composed of several trees, because the search may repeat from multiple sources.

BFS vs. DFS

Doesn’t the BFS tree have back edges as well? ie. edges that exist in the original graph but not in the BFS tree.

There can be edges that exist in the original graph but not in the BFS tree, but the only place these edges can be is between nodes on the same level or between nodes that are one level apart. This means calling them “back edges” is a little misleading since the furthest back they can go is one level.

• True or False. Given a connected undirected graph $G=(V,E)$ with $n$ vertices. After running DFS on $G$ from an arbitrary vertex, we output the vertices in increasing order of their finish time, i.e., an ordering $v_1,...,v_n$ such that $f(v_1)\le f(v_2)\le ...\le f(v_n)$, where $f(v_j)$ is the finish time of vertex $v_j$. This ordering has the following property: when we remove the vertices (and associated edges) according to the ordering one by one, the remaining graph is always connected, i.e., after removing vertices $v_1,...,v_i$, and associated edges from the graph, $v_{i+1},...,v_n$ remain connected for all $i=1,...,n-1$.
  • True. This property is a consequence of the nature of DFS. When DFS is performed on a connected undirected graph, it explores all vertices and edges reachable from the starting vertex. During this exploration, it divides the edges into three types: tree edges, back edges, and forward/cross edges.
  • In DFS, the finish times of vertices represent the order in which vertices finish their exploration. When we order the vertices by their finish times in increasing order, it essentially means that vertices with higher finish times are more “deeply” explored or further away from the starting vertex.
  • When we remove vertices in this order, we are essentially removing them from “outer layers” towards “inner layers” of the graph. Since DFS ensures that each vertex reached is connected to the starting vertex, removing vertices in increasing finish time order maintains this connectivity. Removing vertices in this order guarantees that the remaining vertices are still connected because we are progressively removing vertices from the periphery of the explored region towards the center, ensuring that the remaining vertices are still reachable from each other. Therefore, the statement is true.
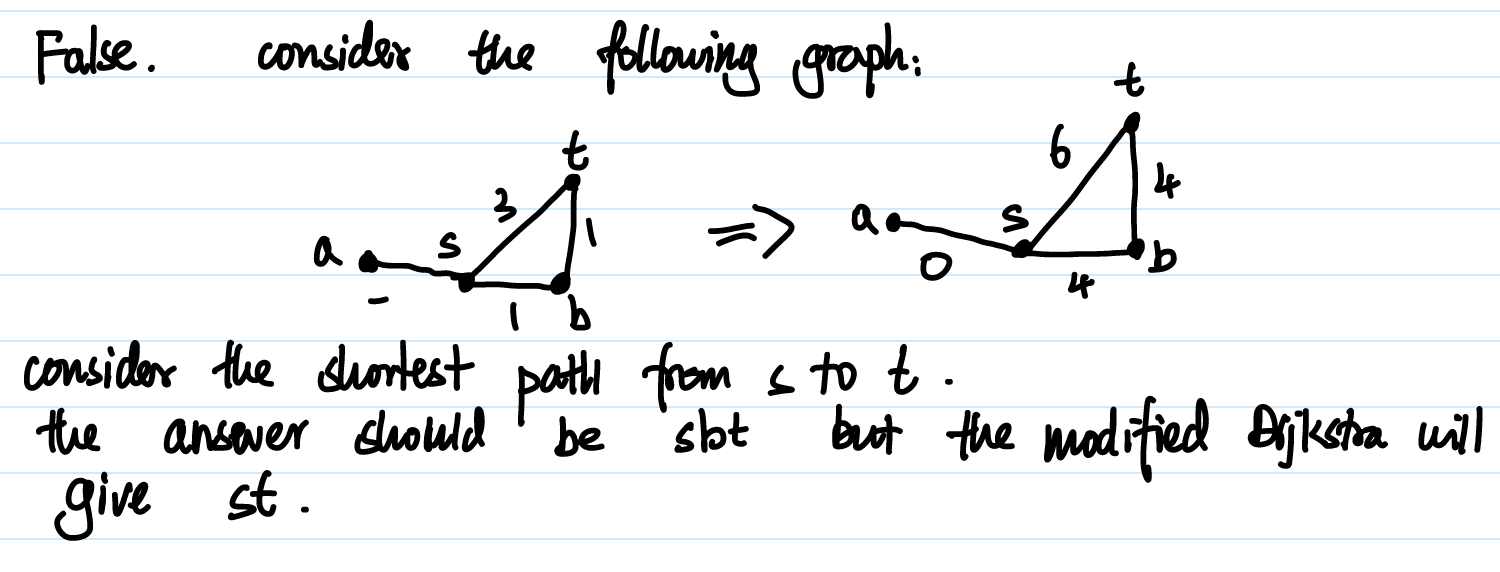
• True or False. Given a directed graph $G$ with possibly negative edge weights $w_e$ (but no negative cycle) and a source vertex $s$, we can apply the following reduction to use Dijkstra’s Algorithm to find single source shortest paths from $s$ to every other vertex: let $w_{min}$ be the minimum edge weight, we modify each edge weight to $w_e^{\prime }=w_e-w_{min}\ge 0$ and then apply Dijkstra’s algorithm to the modified graph with source $s$.
  • False.
  • While it’s true that adding a constant value to all edge weights won’t change the shortest paths (since it just shifts all distances by the same amount), subtracting the minimum weight from all edge weights could potentially make some edge weights negative. This can lead to incorrect results when applying Dijkstra’s algorithm, as it assumes non-negative edge weights.
  • Even though there’s no negative cycle, negative edge weights can still cause issues because Dijkstra’s algorithm greedily selects the vertex with the shortest distance from the source at each step. If negative edge weights are present, this greedy approach may not always yield the correct shortest paths, as it might prematurely select a vertex with a negative edge leading to it, resulting in suboptimal paths.
  • Therefore, while the reduction modifies the edge weights to non-negative values, it doesn’t necessarily preserve the shortest paths, and applying Dijkstra’s algorithm directly to the modified graph can yield incorrect results.
  • 
• True or False. Consider problem SUBSET-GCD-DEC from assignment 10. There exists a polynomial time many-one reduction from SUBSET-GCD-DEC to 3-SAT. Briefly justify your answer.
  • True, 3-SAT and SUBSET-GCD-DEC are both NP-Complete problems. By definition, SUBSET-GCD-DEC ${\le }_p$ 3-SAT. And we believe there exists such a any to one reduction in every known case.
• True or False. Given an undirected graph $G=(V,E)$ with $n$ vertices, let $G^c$ be the complement graph of $G$. We have the following observations: $S\subseteq V$ is a vertex cover of size $k$ in $G$ if and only if $V-S$ is a clique of size $n-k$ in $G^c$. Thus, finding the smallest vertex cover on $G$ is equivalent to find the largest clique in $G^c$. From Lecture 23, we know that there is a 2-approximation algorithm for VERTEX-COVER. (So far, everything is correct, you only need to judge the following statements). If $S$ is a 2-approximation solution for VERTEX-COVER on $G$, then $V-S$ is a 2-approximation solution for CLIQUE on $G^c$. Therefore, we have a 2-approximation algorithm for CLIQUE. Briefly justify your answer.
  • False
• True or False. The following argument shows that Halting problem is decidable. We can solve the Halting Problem with the following algorithm: The input is a program $P$ and input $w$. un $P$ on $w$. If it halts, then output YES. Otherwise, output NO.
  • False

2. Short Answer

• a) Solve the following recurrence with recursion tree method.

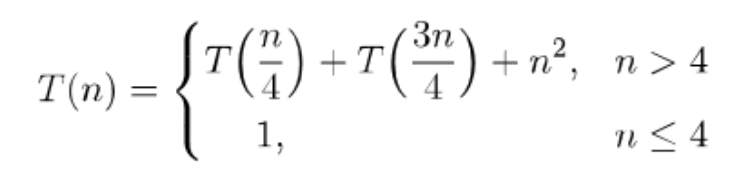
Your answer should be in $\Theta (\cdot )$ form. Show your work on the recursion tree, and briefly justify your $\Theta$ bound.

• b) Given a sorted array of distinct integers $A[\mathrm{1..}n]$, design an $O(\log n)$ time algorithm to check whether there exists an index $i$ such that $A[i]=i$. Briefly describe your idea, then provide your pseudocode. You don’t need to prove correctness or analyze run-time.