Root Locus

Consider an open-loop transfer function

$$L(s)=\text{micro}\frac{N_0(s)}{D(s)}$$

where $N_0(s)$ and $D(s)$ are polynomials of degree $m$ and $n$, respectively.

Definition 11

The root locus for loop gain in the set of all points of the complex plane which are roots of $1+L(s)$ for some $\text{micro}\in (\infty ,0)\cup (0,\infty )$

Basic Rules to draw the root locus for $\text{micro}>0$ are the following:

1. The locus has $n$ branches, one per pole
2. The locus is symmetric with respect to the real axis
3. The branches of the locus start at the poles of $L(s)$
4. For $\text{micro}\to \infty$
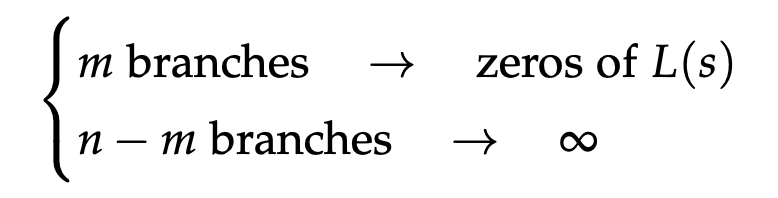
5. The asymptotes of the root locus meet on the real axis at $x_a=\frac{1}{n-m}(\sum _{i=1}^n{p}_i-\sum _{i=1}^m{z}_i)$, $p_i$ and $z_i$ being the poles and zeros of $L(s)$, and have slope ${\xi }_a=\frac{2k+1}{n-m}\pi$, $k=0,...,n-m-1$
6. The locus includes all points of the real axis on the left of an odd number of poles/zeros

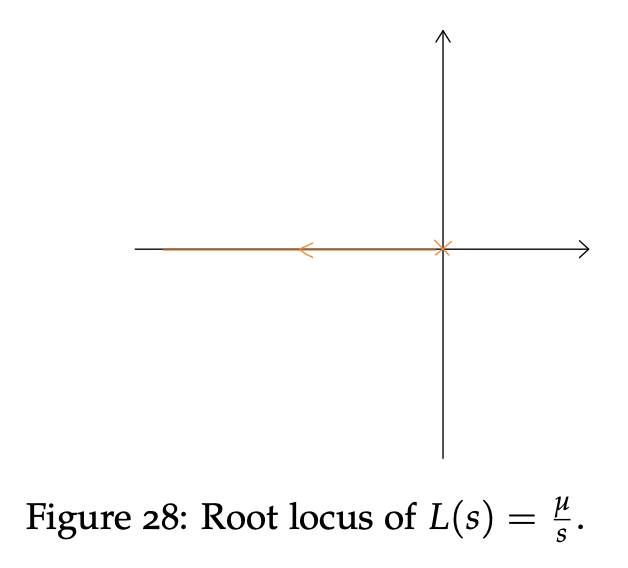
Example 6

The root locus of $L(s)=\text{micro}s$ is shown in Fig. 28. Increasing the gain μ makes the closed-loop system faster and faster. The close-loop system is stable for all μ > 0.

Example 7

todo