Quadtree (Partition Trees)

Quad-tree are partition trees:

• organize space to facilitate efficient multidimensional search
  • internal nodes are associated with spatial regions
  • actual dictionary points stored only at leaves $\to$ quad-tree and kd-Tree.

We have $n$ points $S=(x_0,y_0),(x_1,y_2),...,(x_{n-1},y_{n-1})$ in the plane. We need a bounding box $R=[0,2^{k)}\times [0,2^k)$: a square containing all points. Basically, side length $R$ needs to be a power of $2$.

Structure:

• Root $r$ of the quadtree is associated with region $R$
• If $R$ contains $0$ or $1$ points, then root $r$ is a leaf that stores point.
• Else split: Partition $R$ into four equal subsquares (quadrants) $R_{NE},R_{NW},R_{SW},R_{SE}$
• Partition $S$ into sets $R_{NE},R_{NW},R_{SW},R_{SE}$ of points in these regions.
  • [convention]: points on split lines belong to right/top side
• Recursively build tree $T_i$ for points $S_i$ in region $R_i$ and make them children of the root

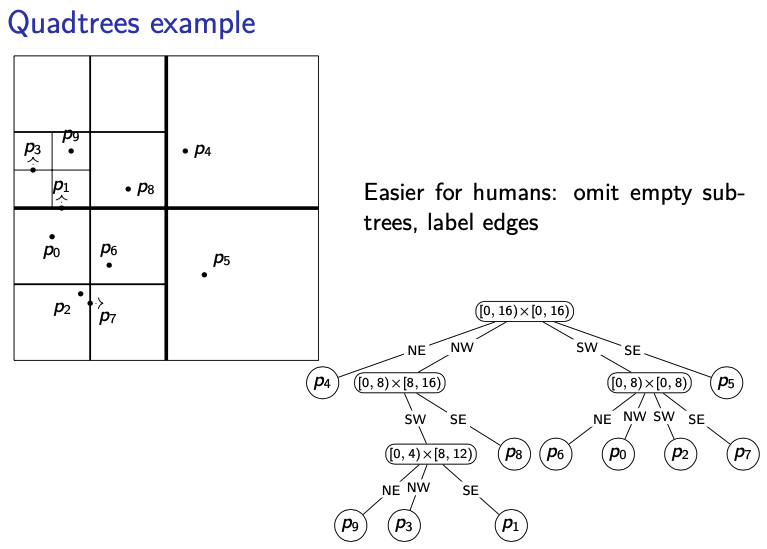
Quadtree Dictionary Operations

• $search$: Analogous to BST and Tries
• $insert$:
  • Search for the point, then
  • Split the leaf while there are two points in one region
• $delete$:
  • Search for the point
  • Remove the point
  • If its parent has only one point left: delete parent (and recursively all ancestors that have only one point left)

Question: why do i delete the parent that has only one point left?

Insert example:

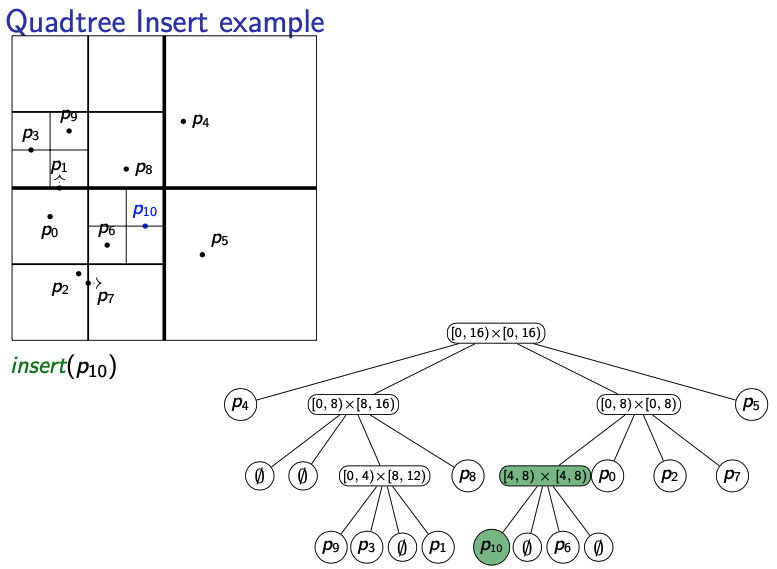
I don’t understand why we put Point10 over there and extend the child P6 to $[4,8)\times [4,8)$.

There are two cases for $Insert$:

• First perform search
• Two cases:

1. search finds a leaf storing one point
   • we need to repeatedly split the leaf while there are two points in one region. since if we insert, there will be two points in the region, so we need to split that subtree until it has one point in each region.
2. search finds an empty subtree
   • then we can just add in the point we want to insert since there are no points there
   • expand empty subtree into a leaf storing insertion point

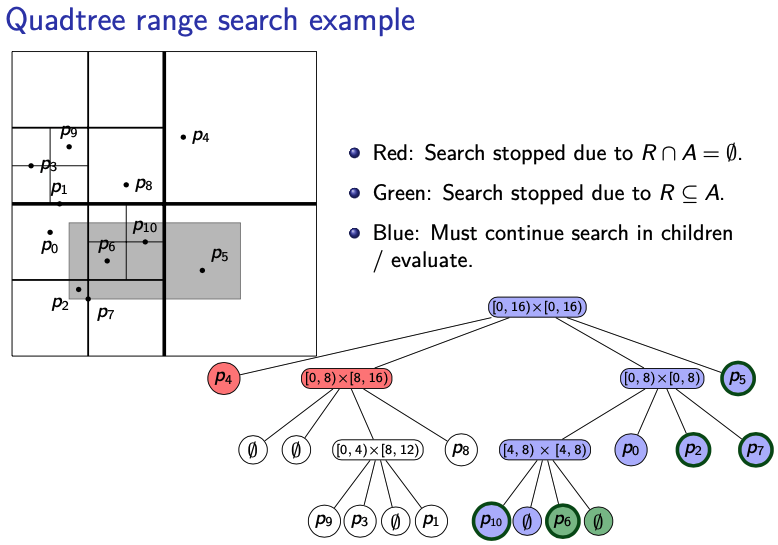
Quadtree Range Search:

Basically, if the region is not in what we are looking for A, we return. Don’t go down. If it’s in the region we must continue the search in children. If it’s a leaf and the point stored is in the region A we are looking for, we return the point.

Note

We assume here that each node of the quadtree stores the associated square. Alternatively, these could be re-computed during the sesarch (space-time tradeoff).

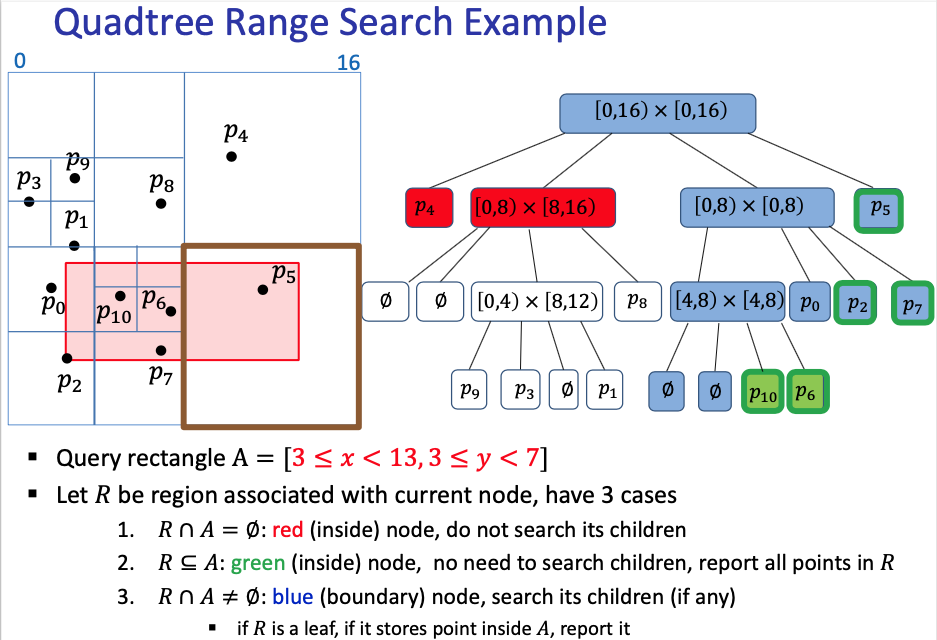
Note

The green outlines are indicating which actual points are returned, whereas the green filled node are ones whose region is fully inside the search area – if a green filled node itself contains a point, it will be outlined and returned, otherwise all of its children are also filled green and follow the same rules recursively.

Range search analysis:

• Running time is number of visited nodes + output size
• No good bound on on number of visited nodes
  • may have to visit nearly all nodes in the worst case
  • $\Theta (nh)$ worst-case

Quad-tree Analysis

What is the height of a quadtree?

• can have very large height for bad distributions of points
• example with just three points, also possible with only two points
• can make height arbitrarily large by moving red points closer together

Quad-tree splits without knowing where the points are.

Height of quad-tree is $\Theta (s)$.

Operations depend on height of tree and the number of points. Number of nodes. Space potentially wasteful, but good if points are well-distributed (not all close together).

Spread factor: $\beta (S):=\frac{sidelengthofR}{dmin}$ We prove $h\in o(\log \beta )$

In the course notes textbook, it says that the we cannot give a bound on the run-time better than the size of the quad-tree, which is $O(nh)$.

• In worst case, height $h\in \Omega (\log (\beta (S)))$
• In any case, height $h\in O(\log (\beta (S)))$
• Complexity to build initial tree: $\Theta (nh)$ worst-case

Questions

Suppose we have a set of 2D points $S=(5,6),(2,1),(0,4),(7,6),(6,2)$. What is the spread factor of the points in $S(i.e\beta (S))$ ?

• 4

Quadtrees divide the 2-dimensional plane into quadrants by splitting a bounded region along lines parallel to the $x$ and $y$ axis. If this idea is extended into 3-dimensions, each internal node would have 16 children.

• False, it would be an Octree, in 3-dimensional space, each internal node would need to be divided into eight octants, not sixteen. Since you split 4 and 4 again when it’s 3d.

If points are chosen correctly, a quadtree of any height $h>0$ can be created containing only 3 points.

• True. How?

Suppose we have a Quadtree of height 3 constructed with initial side length $R$. What is the new maximum height of the tree if we insert a point $(x,y)\in Z^3$ where $x<R$ and $y<R$? (You may assume that the coordinates are integers and the minimum distance between two points is $1$ and that $R>16$.)

• ${\log }_{2}R$, why?

Suppose a quadtree is built using points $P_{1,...,}{P}_k$, where $k=O(1)$ and all points have coordinates in $[0,1]$. If there is a pair of points at distance $1/2^h$ of each other, then the spread factor is $\Omega (2^h)$.

• True, how? Why?

Consider a square region of size $[0,16)$ by $[0,16)$ and a set of distinct points within the region that all have integer coordinates. What is the maximum number of levels that can be in the corresponding quadtree?

• 5 levels, but why?