“University is Hard, Runtime Analysis is Harder”
Run-Time Analysis
Useful: https://www.bigocheatsheet.com/
Running time
The running time of an algorithm on a particular input is the number of instructions and data accesses executed.
We usually denote the running time of an algorithm on an input of size by .
Techniques for Run-time Analysis
- Strategy 1
- Do the analysis of the and obtain a bound for the complexity of the algorithm.
- Strategy 2
- Do the analysis of -bound and a matching -bound separately. Use upper bounds (-bounds) and lower bounds (-bound) early and frequently.
- upper bound: make the number of summands in each sum equal to n
![[Screen Shot 2023-06-22 at 6.42.20 PM.png|]]
- lower bound: to get cubic bound, sufficient to make the number of summands equal to a fraction of .
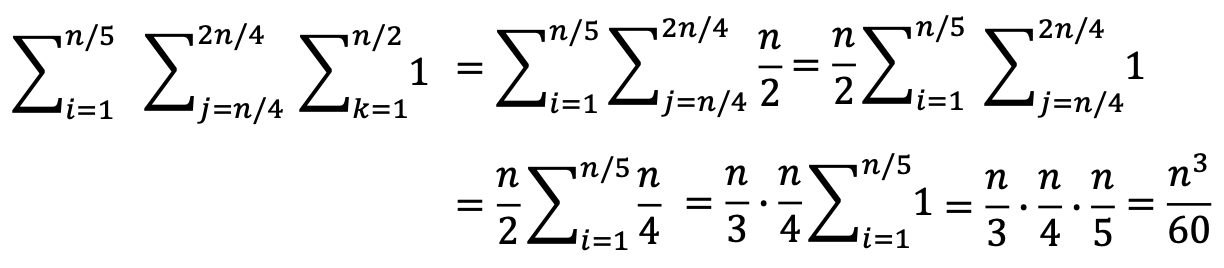
- lower bound: to get cubic bound, sufficient to make the number of summands equal to a fraction of .
- upper bound: make the number of summands in each sum equal to n
![[Screen Shot 2023-06-22 at 6.42.20 PM.png|]]
- Easier because upper / lower bounds are easier to sum.
- Do the analysis of -bound and a matching -bound separately. Use upper bounds (-bounds) and lower bounds (-bound) early and frequently.
Complexity of Algorithms
Important
Cannot make comparisons between algorithms using -notation.
Question
Pseudocode
x = 2000
y = 3142
z = -1
for i from 1 to n:
x = x + 2
for j from i to n:
for k from i to j:
y = y - k
for l from k to j:
z = x + y-
Choose the option which best describes what is sufficient for a complete analysis of the runtime of this pseudocode
- Find a tight and an bound on the runtime (separately)
-
Which option best describes how we set up the expression for the runtime of the algorithm
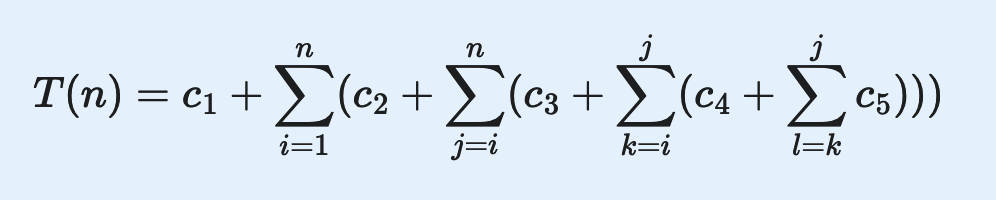
-
Give the expression for the inequality we’d choose to get the bound for the runtime of the algorithm.
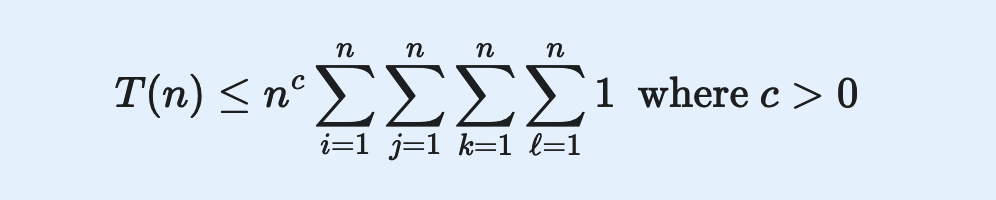
-
How to set up the sum for the bound
- We want the lower bound to look something like this:
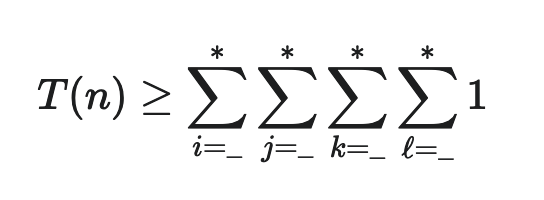 We’ll derive the _ and * bounds for the summation. Start with innermost sum. Since we want a lower bound in terms of , we need to write the innermost as , where . Which of the following conditions must be true in order for .
We’ll derive the _ and * bounds for the summation. Start with innermost sum. Since we want a lower bound in terms of , we need to write the innermost as , where . Which of the following conditions must be true in order for .
- and
- and
- ??????
- We want the lower bound to look something like this:
-
What are the ranges of ?
- but whyy??
-
What is the final bound for the given algorithm?
For analyzing the run-time of algorithms that use recursion, first step is always to derive a Recurrence Relations for the algorithm.
define KNIGHT(A,n):
if n <= 1:
print "Done"
end if
sum = 0
for i from 1 to n:
for j from 1 to n:
for k from j to n:
sum = sum + 2
end for
end for
end for
print sum
KNIGHT(A, n/2)![[Screen Shot 2023-06-23 at 9.59.13 AM.png]]
If $n\leq 1$ we `print DONE` which is 1.
Else, that is if $n > 1$, we have three for loops. That is $\Theta(n^3)+T(n/2)$ because of the last line that calls `KNIGHT(A, n/2)`?
Give a recurrence relation for the following algorithm:
define POINTLESS(A, i, n):
Input: An array A with n items, and where i is initially 1
if n <= 3:
print ":)"
end if
partition_1 = i + (n / 4)
partition_2 = i + (partition_1 * 2)
partition_3 = i + (partition_1 * 3)
POINTLESS(A, i, n/4)
POINTLESS(A, partition_1, n/4)
POINTLESS(A, partition_2, n/4)
POINTLESS(A, partition_3, n/4)
return A- Notice we call POINTLESS four times. and every time pass in . And because assigning partition 1,2,3 takes time. That is for . Otherwise, it’s since it’s just a
printstatement.
When analyzing code with a while loop, such as the following pseudocode
j = n^2
while j > 1:
j = j / 3Since we don’t know anything about the number of iterations of the loop and therefore it’s a bit harder to find out the expression for the runtime. Choose the best strategy:
- Let be the number of iterations of the while loop. We only know that it is a positive integer. Using what we know about the rate of decrease of (initially ) in the loop, we can solve for when and get an expression (inequality) for it in terms of .
Run-time for the following:
s := 0
for i := 1 to n do
for j := 1 to n do
s := s + (i - j)^2- Two for loops (tight bound)
- represent both upper and lower bounds of the algorithm’s time complexity. Provides a tight range in which the algorithm’s growth falls.
A is an array of size n
for i := 1 to n-1 do
j := i
while j > 0 and A[j] < A[j-1] do
swap A[j] and A[j-1]
j := j - 1- two loops,
forandwhile. Outer loop iterates from to , iterations. The innerwhileloop, in worst-case, iterates times for each iteration of the outer loop.
If is the running time of the following code, then what is the tightest lower bound?
x := 0 // Assume n is a power of 2
for i := 1 to 2*log(n^3) do // n to the power 3
for j := 1 to 2^i do // 2 to the power i
x := x + 1- The lower bound of this algorithm is , Outer loop is to and inner loop is to , is the current value of outer loop for each , inner loop does iterations. Since the inner loop is nested within the outer loop, we need to find the max number of iterations for the inner loop across all iterations of the outer loop. So the max value of is . Then, inner loop iterates from to which simplifies to and further simplified to .