Binary Heap

A binary heap is a certain type of Binary Tree. Less strict than a binary tree, each node’s children needs to be smaller or bigger than the parent node. A Binary Heap is another way of implementing a Priority Queue.

A heap is a binary tree with the following two properties:

• Structural Property: all levels of a heap are completely filled, except (possible) for the last level.
• Heap-order Property: For any node $i$, the key of the parent $i$ is larger than or equal to key of $i$. $\to$ max-heap Lemma: The height of a heap with $n$ nodes is $\Theta (\log n)$

Run-time for creating binary heap:

• $\Theta (n)$ using Heapify (bottom-up approach)
• $\Theta (n\log n)$ using insertion? (top bottom approach)

Storing Heaps in Array

Let $H$ be a heap of $n$ items and let $A$ be an array of size $n$. We store the root in $A[0]$ and continue with elements from top to bottom, in each level left-to-right.

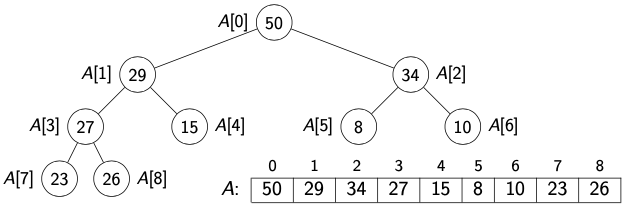
• root $\to$ node at index $0$
• last node $\to n-1$
• left child $\to$ node $2i+1$
• right child $\to$ node $2i+2$
• parent $\to$ node $\lfloor \frac{i-1}{2}\rfloor$

Functions:

• root()
• last()
• parent(i)

Operations in Binary Heaps

Insert

• Place new key at the first free leaf
• Perform fix-up since heap-order might be violated.

Time complexity of insert: $O$(height of heap) $=O(\log n)$

fix-up

Pseudocode:

deleteMax

• The maximum item of a heap is at the root node
• Replace the root by the last leaf (last leaf is taken out)
• The heap-order property might be violated $\to$ fix-down

Time complexity of deleteMax: $O$(height of heap) $=O(\log n)$

fix-down

Pseudocode:

• small node from the top, swap with bigger node

Priority Queue Realization Using Heaps

• Store items in array $A$ and globally keep track of size
• insert and deleteMax $\to O(\log n)$ time

Sorting using heaps

Remember from Priority Queue sorting have time: $O(initialization+n\ast insert+n\ast deleteMax)$ Using binary-heap to implement PQs we have:

• since both insert and deleteMax run in $O(\log n)$ time for heaps
• PQ-Sort using heaps takes $O(n\log n)$ time.

Questions

• Given an array $A$ of $n$ elements, what are the possible runtimes for creating a binary heap from all the elements of  using the algorithms discussed in lecture?
  • $\Theta (n\log n)\to$ Insertion (top-bottom)
  • $\Theta (n)\to$ Heapify
• In a max-heap implemented as an array, an item with the smallest key must be the last valid item in the array.
  • False
• In a max-heap implemented as an array, at least one of the leafs must be an item with the smallest key.
  • True
• Given a max-heap $H$ of $n$ items (implemented as described in class) and a key value $k$, the problem of searching for $k$ in $H$ can be solved in $O(\log n)$ time.
  • False, it is $O(n\log n)$ using PQ-sort.
• In a max-heap implemented as an array, an item with the smallest key may be the strict ancestor of some leaf node (i.e. not the leaf node itself).
  • True, but why?
• In a max-heap implemented as an array, an item with the largest key cannot be a leaf node.
  • False, what if it’s only a root, it is also a leaf?

Related

• Heap Sort $\to$ improved sort of PQsortWithHeaps(A)
• Heapify