MATH213

Midterm MATH213 W24

a. For all $a\in \mathbb{L}$ if, $\mathcal{L}\{f(t)\}=F(w)$ then $\mathcal{L}\{f(\alpha t)\}=\frac{1}{a}F(\frac{w}{a})$

• False

b. If $f$ is a piecewise continuous function, then $f$ is also continuous.

• False

c. ${\int }_{-\infty }^{\infty }{e}^{i\pi x}\delta (x-1)dx=-1$

• True

2. For each DE below state the order of the equation and classify it as PDE or ODE, linear or nonlinear and homogeneous or inhomogeneous.

• a. $y^{\prime \prime }(t)+y^{\prime }(t)=sin(y)$
  • 2nd order, ODE, nonlinear, homogeneous (every term is depending on dep. var. y)
    • why nonlinear?
• b. $u_t(x,t)=-u_x(x,t)+sin(x)$
  • first order, PDE, linear, inhomogeneous

3. Give an example of a IVP that models a system that is dynamic, linear and time-invariant. Briefly explain why your IVP models a system with the given properties.

$$L\frac{di(t)}{dt}+Ri(t)=V(t)$$

Me trying to understand:

• linear: if each term of the equation is with respect to something and its derivatives?
• time-invariant: parameters R and L are constant that has $t$ are constant
• dynamic: system’s behaviour changes with time, as evidenced by the presence of derivatives in the equation

Solution:

• Any linear DE with constant coefficients that has a forcing term works and all needed initial conditions being zero works.
• For a DE of the form $D(y)=f$ where f is the forcing term and D is a linear DE with constant coefficients, the ZIR part of the solution will be

$$y(t)={\int }_0^{t}f(\tau )({\mathcal{L}}^{-1}\{T(s)\}){|}_{t-\tau }d\tau$$

where $T(s)$ is the transfer function.

Clearly the system is dynamic since $y(t)$ depends on all $\tau \le t$, it is linear since the system response to a linear combination of forcing terms is simply the linear combination of the system responses (because the integral is linear), and it is also time-invariant since if we lag the input, a simple change of variables will show that there is a lag in the system response.

4. Compute the two-sided Laplace transform of

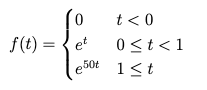
You must explicitly find the ROC with justification.

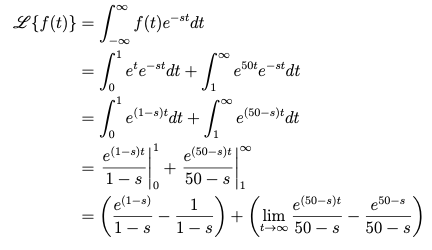
The limit above is only finite when $Re(50-s)<0$ and in this case the limit is simply 0 hence the ROC is $Re(50-s)<0$ or simply $50<Re(s)$. The transform is

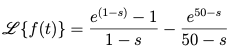
5. Use the Laplace table to compute the Laplace transform of $t{e}^{-2t}sin(2t)+7e^{2t}cosh(\pi t)$. You do not need to determine the ROC. Did it on paper

6. Use the poles to determine if the solution to the DE below is bounded regardless of the initial conditions we choose to apply.

$$y^{(5)}+3y^{(3)}+2y^{\prime }=e^{-t}sin(2t)$$

Solution: The transfer function is

$$T(s)=\frac{1}{s^5+3s^3+2s}$$ $$=\frac{1}{s(s^4+3s^3+2)}$$ $$=\frac{1}{s(s^2+2)(s^2+1)}$$

and the Laplace transform of the forcing term is

$$F(s)=\mathcal{L}\{e^{-t}sin(2t)\}$$ $$=\mathcal{L}\{sin(2t)\}{|}_{s=s+1}$$ $$=\frac{2}{(s+1{)}^2+2^2}$$

For the solution to remain bounded for all possible ICs we need the poles of $T(s)$ to be in the left hand plane or to be of order 1 if they have a real part of zero AND we also need the poles of $T(s)F(s)$ to have the same property.

The poles of T(s) are $0,\pm j,\pm 2j$ and are all of first order and the poles of $F(s)$ are $-1\pm 2j$ and are of first order.

None of these poles have positive real parts, the poles with a real part of 0 are are all of order one, and there is no resonance of the poles of $F$ and $T$ with real part of 0 so the solution will remain bounded.

7. For parts (a) and (b) determine if the Initial and Final Value theorems are applicable to the given function. If they are applicable, apply them and explain the result. If a theorem is not directly applicable, explain why.

You must compute any needed limits but do not need to simply arithmetic computations e.g. unsimplified responses like $\frac{2\times 5\times 6}{3^2}$ are fine.

• a. $F(s)=\frac{s-1}{s(s+1)(s^2+1)}$
• b. $F(s)=\frac{(s-3)(s-2{)}^2(s+1)}{s(s-3)(s+6{)}^3}$

Solution:

a. $F$ is strictly proper rational function, so it has an inverse Laplace transform and hence the IVT and FVT apply.

8. Give the general form for the inverse Laplace transform of

$$F(s)=\frac{1}{s^2(s^2+4{)}^3(s^2-9)}$$

As an example for what is meant by “general form” the general form for the inverse Laplace transform of $\frac{1}{(s+1)(s^2+4)}$ is $A{e}^{-t}+Bsin(2t)+Ccos(2t)$ for some $A,B,c\in R$.

Solution: The standard PF decomposition we need to make is

$$F(s)=\frac{C_1}{s^2}+\frac{C_2}{s}+\frac{C_{3}s}{(s^2+4{)}^3}+\frac{C_{5}s+C_6}{(s^2+4{)}^2}+\frac{C_{7}s+C_8}{s^2+4}+\frac{C_{9}s+C_{10}}{(s^2-9{)}^2}+\frac{C_{11}s+C_{12}}{s^2-9}$$

The inverse Laplace transform of the first two terms is $C_{1}t+C_2$. For the next three terms we note that one and two applications of the multiplication by $t$ rule will transform the Laplace transform of $Asin(2t)+Bcost(2t)$ into the form of the fourth and third terms respectively. Hence the inverse transform of the three terms that include $s^2+4$ term in the denominator will be of the form

$$(D_1+D_{2}t+D_3{t}^3)sin(2t)+(D_4+D_{5}t+D_6{t}^2)cost(2t).$$

Finally a similar analysis of the last two terms but replacing the trig terms with their hyperbolic equivalences yields an inverse transform of the form

$$(D_7+D_{8}t)sinh(4t)+(D_9+D_{10}t)cosh(3t)$$

Putting this together, gives the general form

$$C_{1}t+C_2+(D_1+D_{2}t+D_3{t}^3)sin(2t)+(D_4+D_{5}t+D_6{t}^2)cost(2t)+(D_7+D_{8}t)sinh(4t)+(D_9+D_{10}t)cosh(3t)$$

where the $Cs$ and $Ds$ are constants.

Process:

• Denominator descending and top
• then not too sure

9. Use the convolution theorem to compute $4t^2\ast e^{2t}$ where both functions are one-sided …