Recurrence Relations

A recurrence is an equation that describes a function in terms of its value on other, typically smaller, arguments. Recurrences go hand in hand with the Divide-and-Conquer method because they give us a natural way to characterize the running times of recursive algorithms mathematically.

Three methods of solving recurrences:

• Substitution Method: we guess a bound and then use mathematical induction to prove your guess correct and solve for constants.
• Recursion-tree Method: converts the recurrence into a tree whose nodes represent the costs incurred at various levels of the recursion. We use techniques for bounding summations to solve the recurrence. To solve the recurrence, you determine the costs at each level and add them up.
• Master Method: provides bounds for recurrences of the form $T(n)=aT(\frac{n}{b})+f(n)$, where $a\ge 1,b>1$ and $f(n)$ is a given function. It characterizes a divide-an-conquer algorithm that creates $a$ subproblems, each of which is $1/b$ times the size of the original problem, using $f(n)$ time for the divide and combine steps. To apply the master method, you need to memorize three cases, but once you do, you can easily determine asymptotic bounds on running times for many divide-and-conquer algorithms.

Some Recurrence Relations

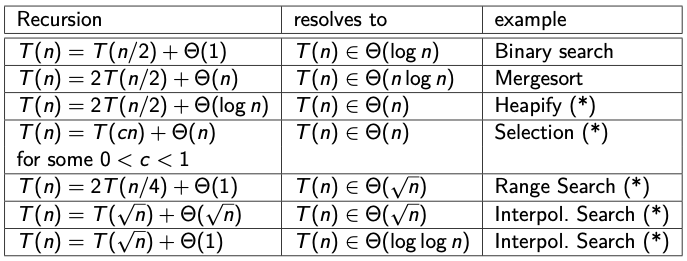
• Usually easy to prove by induction if we know the result

How to Solve Recurrence Relations

I always have difficulty doing that.

Some conventions for recurrences:

We adopt the following convention:

Whenever a recurrence is stated without an explicit base case, we assume that the recurrence is algorithmic.

Substitution Method

The point of using induction in the substitution method is to obtain a result that conforms to the definition of big-Oh, i.e., $\exists n_0$, $c$ such that $f(n)\le cg(n)\forall n\ge n_0$. It follows that the $c$you use in your base case and the inductive step has to be the same, otherwise you can end up proving statements that are in fact incorrect.

Master Theorem

Fairly straightforward.

Recurrence Tree

Height of the tree: https://stackoverflow.com/questions/1347909/how-to-determine-the-height-of-a-recursion-tree-from-a-recurrence-relation

If recurrence is in the form of $T(n)=aT(n/b)+f(n)$ then the depth of the tree is log base b of n.

For example, $2T(n/2)+n$ recurrence would have tree of depth $\log (n)$ (log base 2 of n).

Helps with guessing.