CS341

Study CS341

Final W2021

1

• True or False. Given an array A of n integers, there is no linear time algorithm to find the k-th smallest element in A. Briefly justify your answer.
  • False. There are linear time algorithms to find the k-th smallest element in an array A of n integers, such as the Quickselect Algorithm. QuickSelect is an efficient algorithm based on the quicksort paradigm, which can find the k-th smallest element in expected linear time O(n) on average. It achieves this by partitioning the array similar to quicksort but only recursively exploring the partition that contains the desired element, effectively reducing the search space by half at each step.
• True or false. If a tree T is both DFS tree and BFS tree of an undirected graph G, then G=T. Briefly justify your answer.
  • True. Suppose $G\ne T$, then $G$ can’t be a tree (otherwise $G=T$). There will be a cycle in $G$. Say it is $v_1{v}_2...v_k{v}_1$. We claim that the BFS and DFS will be different. WLOG, say now visit $v_1$ in BFS and DFS, and it’s the first vertex we encounter in the loop.
  • BFS will give a structure: $v_1-v_2-...-v_k$, all the way to $v_k$. However, DFS will branch at $v_1$. Thus, the BFS and DFS can’t equal in this case.
  • If there exists a cycle in the graph G, then BFS and DFS will produce different structures for the tree T. This is because BFS explores vertices level by level, while DFS explores vertices along paths, and encountering a cycle will lead to branching in DFS. Therefore, if G contains a cycle, T cannot be both the DFS tree and BFS tree of G. So, the statement is indeed true.

2. Short Answer

• b) Given a sorted array of distinct integers $A[\mathrm{1..}n]$, design an $O(\log n)$ time algorithm to check whether there exists an index $i$ such that $A[i]=i$. Briefly describe your idea, then provide your pseudocode. You don’t need to prove correctness or analyze run-time.
  • Use similar approach as Binary Search. Look at the mid element first. If $A[i]=i$, return true. If $A[i]<i$, then repeat on larger half, otherwise, perform on lower half.
  • Pseudocode

A[1..n]
i=1, j=1
while(i <= j)
	mid = (i+j)/2
	if A[mid] = mid
		return true
	else if A[mid]<mid then
		i = mid + 1
	else
		j = mid - 1
end while
return false

3. Greedy

Suppose we are given an array of positive integers $A=[a_1,...,a_n]$ and a cap value $C$. We want to partition the array into minimum number of contiguous blocks such that each block has sum at most $C$.

Example. $A=[2,7,1,4,2,2,2,2,2,3]$ and $C=10$. Then, one optimal solution is to divide $A$ into 3 blocks: $[2,7,1],[4,2,2,],[2,2,2,3]$, where the sums of the blocks are $10,8,9$.

• a) Consider a greedy strategy where we repeatedly select the longest contiguous subsequence $[a_i,a_{i+1},...,a_j]$ with a sum at most $C$ that does not overlap with the previously selected blocks. Provide an example to show that this greedy strategy does not always produce an optimal solution.

  • Here is a counterexample, let’s say we have $A=[1,5,4,5,1,3]$, with $C=10$. The strategy given will separate it in 3 blocks: $[1,5],[4,5],[1,3]$. However the optimal solution would be having 2 blocks: $[1,5,4],[5,1,3]$.

• b) Design a Greedy Algorithm to solve this problem.

Pseudocode

def partition_blocks(A, C):
    blocks = []
    current_block = []
    current_sum = 0
    
    for a in A:
        if current_sum + a <= C:
            current_block.append(a)
            current_sum += a
        else:
            blocks.append(current_block)
            current_block = [a]
            current_sum = a
    
    blocks.append(current_block)
    
    return blocks
 
# Example usage:
A = [2, 7, 1, 4, 2, 2, 2, 2, 2, 3]
C = 10
print(partition_blocks(A, C))

Idea: The approach of this greedy algorithm is to iteratively construct blocks such that each block has a sum at most $C$, while minimizing the number of blocks used.

The idea is to traverse the array of integers $A$ and maintain a current block. At each step, we add elements from $A$ to the current block as long as the sum of the current block remains less than or equal to $C$. If adding an element would exceed the sum $C$, we finalize the current block, append it to the list of blocks, and start a new block with the current element.

This process continues until we have traversed all elements of $A$. The resulting list of blocks represents the partition of $A$ into contiguous blocks, each with a sum at most $C$. By constructing blocks greedily in this manner, we aim to minimize the total number of blocks required to satisfy the given constraint.

We start from the beginning of the array, then get the largest contiguous subsequence $[a_1,a_2,...,a_k]$ with a sum at most $C$ then repeatedly doing this until we reach the end.

Pseudocode:

A[1...n], C
start = 1, sum = 0
for end from 1 to n do:
	if sum + A[end] > C then:
		addBLock(A[start...end-1])
		sum = 0
		start = end
	end if
	sum = sum + A[end]
end for

The provided pseudocode outlines a greedy algorithm to partition the array AA into contiguous blocks with sums at most CC. Here’s a brief explanation of the approach:

1. Initialize variables start=1start=1 (indicating the start index of the current contiguous subsequence) and sum=0sum=0 (indicating the sum of the current contiguous subsequence).
2. Iterate over each element of the array AA from index 1 to nn:
   • If adding the current element to the current sum exceeds CC, it means that the current contiguous subsequence has reached its maximum sum. Therefore, add the current contiguous subsequence (from index start to end−1) as a block, reset the sum to 0, and update the start index to end.
   • Otherwise, add the current element to the sum.
3. After iterating through all elements, add the remaining contiguous subsequence (if any) as the last block.

This algorithm effectively partitions the array into contiguous blocks with sums at most $C$ by greedily selecting the largest contiguous subsequence at each step. This approach ensures that the number of blocks used is minimized.

4. Dynamic Programming

We consider a variant of the 0/1-Knapsack Problem in Lecture 10. Suppose there are $n$ items $1,...,n$ that come in a sequence. Each item has a weight $w_i$ and a value $v_i$ (both $w_i$ and $v_i$ are nonnegative integers). You are given a knapsack of size $W$ (a nonnegative integer), and the task is to select a subsequence of items with increasing values to maximize the total value while satisfying the capacity constraint. Formally, we want to find a subsequence $1\le i_1<...<i_k\le n$ to maximize the total value $\sum _{j=1}^k{w}_{i_j}$ subject to the constraints $\sum _{j=1}^k{w}_{i_j}\le W$ and $v_{i_1}\le v_{i_2}\le ...\le v_{i_k}$. Example. Let $(w_1=2,v_1=5),(w_2=3,v_2=2),(w_3=2,v_3=4)$ be three items, and the capacity of the knapsack is $W=7$. Although the capacity of the knapsack is enough for all three items, the optimal solution of this example can only pick the last two items, i.e., $i_1=2,i_2=3$, with total value $6$.

Design a dynamic programming algorithm to compute the optimal value of the above problem. Your algorithm should run in time polynomial in $n,W$ and $V:=ma{x}_{1\le i\le n}{v}_i$ (i.e., the maximum value of an item).

Your solution must consist of:

• A description of the subproblems you will solve and the order in which you will solve them.
• A formula for solving one subproblem in terms of previously solved subproblems, and a justification of correctness.
• Pseudocode of your algorithm
• An analysis of run-time using big-O notation.

Subproblems: $M[i,w]$: the optimal solution we can get with weight $w$, and with item $i$ picked. This means $v_i$ is the highest value we’ve seen so far. We will solve them from bottom-up so $i=1$.

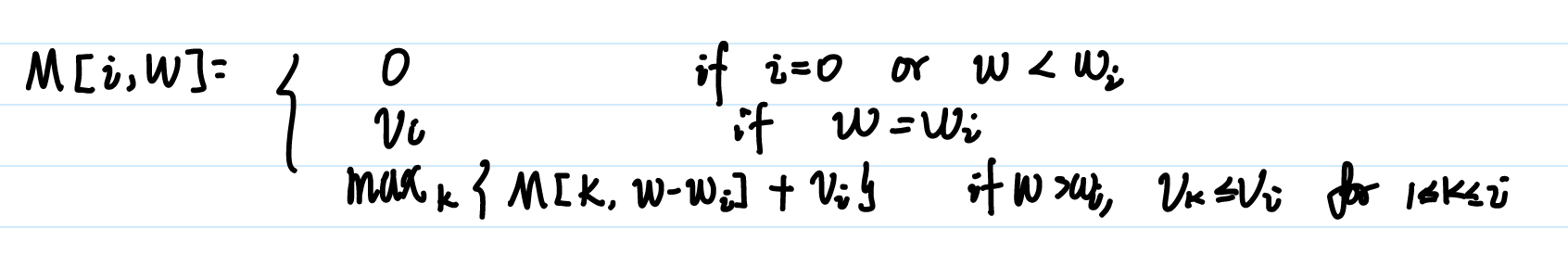
The base case is trivial as we defined, since we cannot choose anything if weight limit is 0.

Consider $M[i,w]$, since we must choose $i$, if $w<w_i$, we cannot choose any item. If $w=w_i$ then we can only choose $i$.

For $w>w_i$, before we choose $i$, the bag has a limit of $w-w_i$. And, we will only consider previous item $k$ with $v_k\le v_i$ to permit our property.

Consider the max value we can get: $O(i,w)$.

$$O(i,w)=v_i+O(j,w-w_i)$$ $$\le v_i+ma{x}_k\{M[k,w-w_i]\}$$ $$=ma{x}_k\{M[k,w-w_i]+v_i\}$$

which is given by our formula.

• $O(j,w-w_i)$ is an optimal selection at some $j$
• second line: for $v_k\le v_i$

Then, to find the real optimal at item $i$, we do $ma{x}_k\{M[i,w]\}$ for $1\le k\le i$ since if we choose some item, then the sequence must end with some item between $1$ and $i$.

Pseudocode:

Use table M[0...n][0...W]
Initialize M[0,w]:= 0 for w=0...W
for i from 1 to n do:
	for w from 0 to W do:
		if w_i > w then do:
			M[i,w] = 0
		else do
			M[i,w] = v_i
			for k from 1 to i-1 do:
				if v_k <= v_i then do:
					M[i,w]:= max{M[i,w], M[k, w-w_i] + v_i}
				end if
			end for
	end for
end for

ans:= 0
for i from 1 to n do:
	ans:= max(ans, M[i,W])
return ans

The runtime is $O(nW\cdot n+n)=O(n^{2}W)$

• $nW$: number of subproblems
• $\cdot n$: runtime to solve each subproblem
• $+n$: final step

Wrapping my head around this

Subproblems:

• Define subproblems $M[i,w]$ as the optimal solution with weight ww and item $i$ picked, where vivi​ is the highest value seen so far.
• Solve subproblems bottom-up, starting from $i=1$.
• Base case: $M[0,w]=0$ for $w=\mathrm{0...}W$ (no items can be chosen if weight limit is 0).

Formula for Solving Subproblems:

• For $w<w_i$, we cannot choose any item.
• For $w=w_i$​, we can only choose item ii.
• For $w>w_i$, consider the maximum value achievable by including item ii or not:
  • $O(i,w)=v_i+ma{x}_{k}M[k,w-w_i]$ where $k$ iterates over previous items with $v_k\le v_i$​.

Pseudocode:

• Initialize table $M[\mathrm{0...}n][\mathrm{0...}W]$ with base cases.
• Iterate over items ii and weights ww, updating $M[i,w]$ using the provided formula.
• Compute the maximum value achievable by considering $M[i,W]$ for $1\le i\le n$.

5. Graph Algorithms

In the Australian outback, imagine a network of feeding grounds for kangaroos. Each feeding ground is modelled by vertices, and if there is a trail between two feeding grounds it is modelled by an undirected edge. Each edge is weighted with the height of the tallest fence along the trail, in meters, or 0 if there is no fence at all.

Describe a preprocessing algorithm that produces in $O(n^3)$ time a data structure for the following task: given a pair of feeding grounds $u$ and $v$, determine in $O(1)$ time whether or not it is possible for a kangaroo that is able to jump over fences of height at most $h$ to get from feeding ground $u$ to feeding ground $v$ (possibly going through other feeding grounds along the way). Note that all of $u,v$ and $h$ are arbitrary.

Hint: consider dynamic programming.

If you are using dynamic programming, your solution must consist of:

• A description of the subproblems you will solve and the order in which you will solve them.
• A formula for solving one subproblem in terms of previously solved subproblems, and a justification of correctness.
• Pseudocode of your algorithm
• An analysis of run-time using big-O notation.

Solution:

We will use a 2-d array $M[u,v]$ to store the lowest fence weight among the highest fence height a of each path from $u$ to $v$.

This question is equivalently asking if there exists a $uv-$path such that the highest weight of an edge along the path is no greater than $h$.

My understanding so far

• Description of Subproblems: You define a subproblem as determining the lowest fence weight among the highest fence heights of each path from feeding ground uu to feeding ground vv.
• Order of Solving Subproblems: The subproblems are solved using dynamic programming, where you compute the lowest fence weight among the highest fence heights for all pairs of feeding grounds uu and vv. This is done using a bottom-up approach.
• Formula for Solving Subproblems: The lowest fence weight among the highest fence heights for a path from uu to vv can be computed by considering all intermediate vertices ww and selecting the maximum of the lowest fence weight among the highest fence heights for paths from uu to ww and from ww to vv, and the weight of the edge connecting uu and vv.

Subproblems: $M_i[u,v]$ is the lowest among the largest weight of each $u,v-$path, with the condition that the path can only use vertices $\{1,2,...,i,u,v\}$.

Suppose the modelled graph is $G(V,E)$. We solve subproblems $M_i[u,v]$ for all $u,v$ as $i$ goes from 0 to $n$.

• $M_0[u,v]=0$, if $u=v$.
• $M_0[u,v]=w(u,v)$, if $(u,v)\in E$
• $M_0[u,v]=\infty$, otherwise

Formular

• $M_i[u,v]=min=max\{m_{i-1}[u,i],M_{i-1}[i,v]\}$
• $M_i[u,v]=min\{M_{i-1}[u,v]\}$

Proof: ? Do i need to do it?

Pseudocode:

Initialize M[u,v] as above
for i from 1 to n do:
	for u from 1 to n do:
		for v from 1 to n do:
			temp:= max{M[u,i], M[i,v]}
			M[u,v]:= min{temp, M[u,v]}
		end for
	end for
end for

input: u,v,h
	if M[u,v] > h: return false
	else: return true.

• Iterate over all possible intermediate vertices $i$ from 1 to $n$, where $n$ is the total number of vertices.
• For each pair of vertices $u$ and $v$, update $M[u,v]$ by considering all possible intermediate vertices $i$.
• Compute the lowest weight of the heaviest edge along the path from $u$ to $v$ by taking the minimum of the maximum weights of the paths from $u$ to $i$ and from $i$ to $v$, considering all possible intermediate vertices $i$.
• Once the preprocessing step is completed and $M[u,v]$ values are computed for all pairs of vertices, you can answer queries in constant time.
• Given a query with vertices $u$ and $v$ and a maximum fence height $h$, check if $M[u,v]$ is greater than $h$. If it is, then it’s not possible for a kangaroo to jump from $u$ to $v$ with a maximum fence height of $h$. Otherwise, it is possible.

Runtime: $O(n^3)$ (triple loop, constant operation in each iteration)

OH I see.

From all the path $u,v$, we look for the lowest of all the heaviest on all paths $u$ to $v$.

We do this for every single $u,v$ path in the graph. Insane.

6. NP-completeness

Recall that a literal is either $x$ or $\neg x$ for some Boolean variable $x$. We say that literals in the form of $x$ are positive, and literals in the form of $\neg x$ are negative.

Prove the following special case of TRUE-FALSE-SAT in Assignment 10 is NP-Complete.

POSITIVE-TRUE-FALSE-SAT

• Input: $n$ Boolean variables $x_1,...,x_n$, $m$ clauses $C_1,...,C_m$, where each contains an arbitrary number of positive literals.
• Output: Does there exist a True/False assignment to $x_1,...,x_n$ such that all the $m$ clauses contain literals with different truth values? (YES or NO)

Examples.

• $(x_1\vee x_2)\wedge (x_3\vee x_4)$ is a YES-instance, where the assignment $(x_1=T,x_2=F,x_3=T,x_4=F)$ is a YES-witness.
• $(x_1\vee x_2)\wedge (x_2\vee x_3)\wedge (x_3\vee x_1)$ is a NO-instance. We can check that there is no assignment that can satisfy the required condition.

Solution:

To prove that POSITIVE-TRUE-FALSE-SAT is NP-Complete, we need to show two things:

1. POSITIVE-TRUE-FALSE-SAT is in NP.
2. POSITIVE-TRUE-FALSE-SAT is NP-hard, meaning every problem in NP can be reduced to it in polynomial time.

i) certificate: an assignment of $x_1..x_n$ verification: We check each clause with the assignment to see if it contains one true and one false. We can also check along the way that every literal is positive. If every clause has one true and one false, then YES. We only loop once so polynomial time.

ii) We use TRUE-FALSE-SAT

TRUE-FALSE-SAT ${\le }_p$ POSITIVE-TRUE-FALSE-SAT

iii) Input Transformation: input: $n$ Boolean variables $x_1,....,x_n$, $m$ clauses $C_1,...,C_n$.

Construct an input as follows:

• For each $x_i$, we add an auxiliary variable $y_i$ and add a clause $C_i^{\prime }=(x_i\vee y_i)$. Then check each clause $C_i$.
• If we found a negative literal say $\neg x_j$, then we substituted it with $y_j$.

iv) Proof:

• $\Rightarrow$ Assume there is an assignment $x_1...x_n$ such that each clause contains literals with opposite truth values.
  • Then wee use the same assignment $x_1,...,x_n$ and assign each $y_i$ to be $\neg x_i$. i.e. $y_i=\neg x_i$.
  • Then, for $C_i$, since wee simply substitute $\neg x_i$ with $y_i$, and now $y_i=\neg x_i$, the assignments of these clauses remains the same. Therefore, there is at least one tru and one false in each $C_i$.
  • Consider $C_i^{\prime }=(x_i\vee y_i)$ since $y_i=\neg x_i$. $C_i^{\prime }$ has exactly one true and one false.
  • Therefore, there exists an assignment $x_1,...,x_n$, $y_1,...,y_n$ such that all the $C_i,C_i^{\prime }$ clauses contain literals with different values. i.e. a YES for POSITIVE-TRUE-FALSE-SAT.
• $\Leftarrow$ Assume that there exists an assignment $x_1,...,x_n$, $y_1,...,y_n$ such that all the $C_i,C_i^{\prime }$ clauses contain literals with different values.
  • For $C_i^{\prime }=(x_i\vee y_i)$, since it contains literals with different values, then $x_i=\neg y_i$ or $y_i=\neg x_i$ in the assignment.
  • Then, for each $C_i$, we replace $y_i$ with $\neg x_i$. Since $C_i$ contains literals with different values and $y_i=\neg x_i$, we are not changing any values in the substitution, thus each $C_i$ contains different values.
  • Therefore, a YES for TRUE-FALSE-SAT.

v) We only need to make a new variable and one new clause for each $x_i$. And check each clause to substitute once. This can be done in polynomial time.

7. Exchange Algorithm for MST

We have seen that actually: https://piazza.com/class/lr45czd8jab7cz/post/1265, according to this piazza post…

Note:

This is intended to be a harder question. Your answer will be marked based on the elegance of your proof and the quality of your bound. If you are short of time, or having difficulties, we recommend skipping this question.

Given an undirected connected graph $G=(V,E)$ with $n$ vertices and $m$ edges. The edges in $G$ are associated with pairwise distinct edge weights $w_e,e\in E$. We consider the following exchange algorithm for finding Minimum Spanning Tree (which is less efficient than Kruskal’s Algorithm and Prim’s Algorithm).

Exchange
	Let T be an arbitrary spanning tree of G.
	while there exists (e,e') that admits a valid exchange and w(T - e + e') < w(T)
		T:= T - e + e'
	return T

Hint: you may find some minimum spanning tree properties in Assignment 6 useful.

• a) Prove that Exchange returns a minimum spanning tree of $G$ when it terminates.
• b) Show that the algorithm always terminates by providing an upper bound on the number of iterations in terms of $m$ and $n$.

Midterm F2023

Problem 4 - Greedy

The input is an unsorted sequence of integers $v_1,...,v_n$ representing the values of some collectible assets, and a number of years $k\le n$. At the start of each year you get to collect one of theses assets, and add it to your investment portfolio. At the end of each year, the total value of your entire investment portfolio doubles. (It starts at 0)

So for example, if at the start of the year you have a portfolio that is worth 100 dollars, and you collect a new asset worth 20 dollars, at the end of the year your portfolio is worth 240 dollars.

• 1. Give a greedy algorithm to solve this problem. It should output the value of your portfolio after $k$ years.

FindGreedyPortfolioValue(v, k)
v <- sort v by value of v_i in non-decreasing order
profit <- 0
for i from 1 to k do:
	profit = profit + v[i]
	profit = profit x 2
end for
return profit

• 2. Analyze the runtime of your algorithm in the unit cost model.
  • Due to the for loop we have $O(1)$ operations and the sorting take $O(n\log n)$ time. Thus the runtime is $O(k+n\log n)$.
• 3. Prove your algorithm is correct (i.e., optimal).

To prove the correctness of the algorithm, we need to show that it always produces the maximum possible portfolio value after $k$ years.

Let’s consider the algorithm’s strategy:

1. Sorting: The algorithm sorts the assets in non-decreasing order of their values. This ensures that the assets with the highest values are collected first.
2. Collecting Assets: For each year $i$ from 1 to $k$, the algorithm collects the asset with the $i$-th highest value available. After collecting an asset, the total value of the portfolio is doubled.

The correctness of the algorithm can be proven by induction on the number of years $k$.

Base Case ($k$ = 1):

• When $k=1$, the algorithm collects the asset with the highest value available. This results in the maximum possible portfolio value after 1 year, as there is only one asset to collect.

Inductive Step:

• Assume that the algorithm correctly selects assets to maximize the portfolio value after $k-1$ years.
• In the $k$-th year, the algorithm collects the asset with the $k$-th highest value available. Since the assets are sorted in non-decreasing order, this is the $k$-th highest value overall. Therefore, the portfolio value after $k$ years is maximized by this selection.
• Doubling the portfolio value at the end of each year ensures that the total value after kk years is maximized.

Since the algorithm selects assets in a way that maximizes the portfolio value after each year, it follows that the overall portfolio value after $k$ years is also maximized. Therefore, the algorithm is correct (i.e., optimal).

Problem 5 - DP

Let $A=(a_1,...,a_n)$ be a sequence of distinct positive integers. We say that a subsequence $a_{i_1},...,a_{i_k}$ is legal if it includes at least one element from every two consecutive elements in $A$, and it includes the last element of $A$. Formally, $i_1\le 2,\forall j\in \{1,...,n\}:i_{j+1}\le i_j+2$ and $a_{i_k}=a_n$.

For example, given the sequence $(5,6,7,9,8)$, the subsequence $(5,7,9,8)$ is legal while $(5,9,8)$ is not.

In this question, given a sequence $A=(a_1,...,a_n)$, we would like to find a legal subsequence which has minimum value, where the value of a subsequence is defined as the sum of its elements. For example, for the sequence above, the subsequence $(5,7,8)$ is an optimal solution with value 20.

• 1. Prove or disprove: For any $n\ge 4$ and any sequence $A=(a_1,...,a_n)$, if $a_{i_1},...,a_{i_k}$ is a legal subsequence with minimum value, then it does not include two consecutive elements of the original sequence.

False, Consider $A=(1,3,2,4,5)$.

Must contain 5 since it’s the last element. Now all the pairs: $(1,3),(3,2),(2,4)$. So the legal subsequence with minimum value is $(1,2,4,5)$ and includes two consecutive elements that is 2 and 4 from the original sequence.

• 2. Given sequence $A=(a_1,...,a_n)$, let $B[1,...,n]$ be an array such that $B[i]$ is the minimum value of a legal subsequence of $(a_1,...,a_i)$. Write a recurrence relation for $B[i]$. You can assume that $B[0]=B[-1]=0$.
• 3. Write detailed pseudocode for an algorithm that takes as its input a sequence $A=(a_1,...,a_n)$ and returns the minimum value of a legal subsequence.

FindMinLegal(A(a_1,...,a_n)):
    s <- dp table of size (n+1)
    s[0] <- 0
    for i in (1...n) do:
        if (i == 1):
            s[i] = a_1
        else if (s[i-1] >= s[i-2]):
            s[i] = a_i + s[i-2]
        else if (s[i-1] < s[i-2]):
            s[i] = a_i + s[i-1]
    return s[n]

This algorithm initializes the dynamic programming table s with size (n+1) and computes the minimum value of a legal subsequence ending with each element of A. It uses dynamic programming to store the minimum values in the table s. Finally, it returns s[n], which represents the minimum value of a legal subsequence ending with the last element of A.

Understanding

Ohhhh I see, kinda slowly.

So at first, I was confused to why we compare s[i] values, but notice first line of the algo, we initialize s, as a dp table which creates and store the values of A. It will serve as storing the minimum value of legal subsequence at different length $i$.

Another thing, is in the main loop, we slowly compute the minimum subsequence at each i. So that is why we always add $a_i$ which was something else I was confused about. So we slowly build up our dp table up to $n$, the actually value we care about, which we return.

That is why, we update s[i] for every loop. We return $s[n]$, which represents the minimum value of a legal subsequence actually ending with the last element of $A$.

• 4. Analyze the running time of your algorithm from part iii) in the unit cost model. The table is of the size $n$. Going over the table should take $O(n)$ time only due to the for loop that only does $O(1)$ operation.

Final S2018

True or False

• Any tree with at least 7 vertices must have a vertex degree at least 3.
  • False
  • Consider the graph
  • This graph is a tree, but each vertex has degree at most 2.
• Let $G=(V,E)$ be a directed graph and let $T$ be any DFS tree of $G$. Then for any edge $(u,v)\in E$ that is not in$T$ we must have $PRE[u]>PRE[v]$.
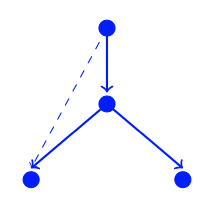
  • False. We can have an edge from an ancestor to a descendent like the dashed line below in DFS.
• Recall that we can modify BFS to check if a graph is bipartite. We can also modify BFS to check if a graph is tripartite. A graph $G=(V,E)$ is tripartite if there are disjoint sets of vertices $V_1,V_2,V_3$ such that $V_1\cup V_2\cup V_3$ and $\forall (u,v)\in E$, $u,v$ are not in the same set $V_i$.
  • False. A tripartite graph is the same as a 3-Colourable graph, and 3-Colourable is NP-complete.
• The complement independent set $S\subseteq V$

HW 2023