Knapsack Problem

gap-in-knowledge Video on how to compute the table: https://www.youtube.com/watch?v=nLmhmB6NzcM (understand)

From CS341

We’ve only looked at 0/1-KnapSack.

Input:

• items $1,...,n$ with weights $w_1,...,w_n$ and values $v_1,...,v_n$
• a capacity $W$

Output:

• a choice of items $S\subset \{1,...,n\}$
• that satisfies the constraint $\sum _{i\in S}{w}_i\le W$
• and maximizes the value $\sum _{i\in S}{v}_i$

Example:

• $w_1=3,w_2=4,w_3=6,w_4=5$
• $v_1=2,v_2=3,v_3=1,v_4=5$
• $W=8$
• optimum $S=\{1,4\}$ with weight $8$ and value $7$

See also:

• fractional knapsack (items can be divided), solved with a greedy algorithm

Note

• We want to respect the weight constraint of the chosen items $w_i\le W$ by optimizing the number of elements we put in.
• Does this have the constraint of only being able to pick an item once?
• In Fractional Knapsack, we can break items for maximizing the total value of the knapsack.

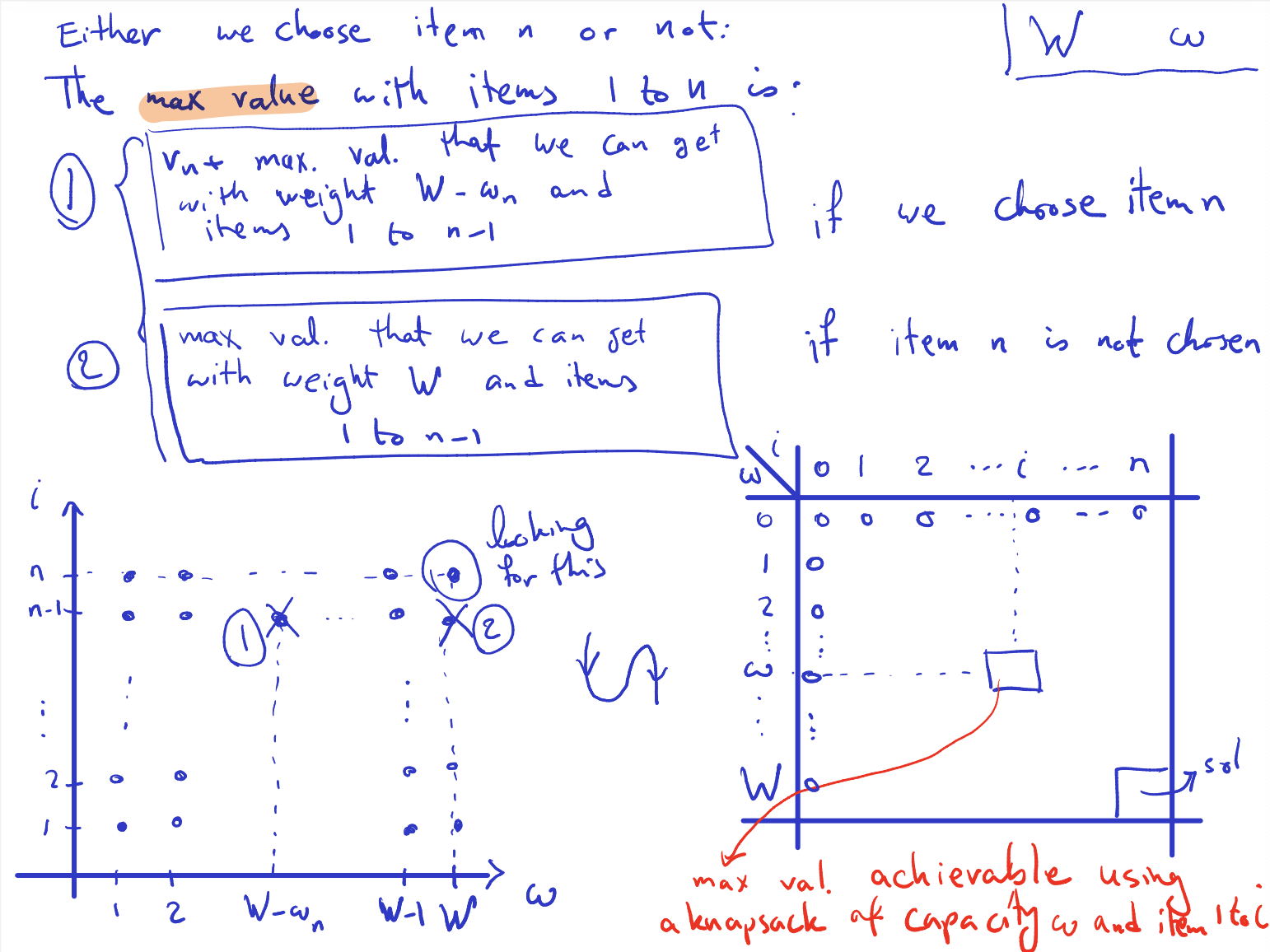
Setting up the recurrence

Basic idea: either we choose item $n$ or not.

• then the optimum $O[W,n]$ is the max of two values:
• $v_n+O[W-w_n,n-1]$, if we choose $n$ (and $w_n\le W$)
  • Choosing item $n$: If we choose item $n$, we add its value $v_n$ to the total value. After choosing item $n$, we reduce the available capacity of the knapsack by the weight of item $n$, which is $(W-w_n)$. This means we now have to consider the remaining items (from $1$ to $(n-1)$) with the reduced capacity.
  • Indexing for remaining items: In dynamic programming, when considering the subproblems, we often index the items from $1$ to $n$. So, if we choose item $n$, we need to consider the subproblem with items $1$ to $(n-1)$ (i.e., excluding item $n$) to find the maximum value achievable with the reduced capacity.
• $O[W,n-1]$, if we don’t choose $n$

$O[w,i]:=$ maximum value achievable using a knapsack of capacity $w$ and items $1,...,i$

Initial conditions

• $O[0,i]=0$ for any $i$
• $O[w,0]=0$ for any $w$

Summary

Therefore, the term "$O[W-w_n,n-1]$" represents the maximum value achievable with the remaining capacity $(W-w_n)$ considering only the first $(n-1)$ items, which is why it’s $(n-1)$ and not $n$. We exclude item $n$ from consideration after choosing it for the knapsack.

Algorithm

• it should be in the else $v_i$ and $w_i$ instead of $j$s.

Discussion:

This is called a pseudo-polynomial algorithm

• in our word RAM model, we have been assuming all $v_i$s and $w_i$s fit in a word
• so input size is $\Theta (n)$ words
• but the runtime also depends on the values of the inputs

01-knapsack is NP-Complete, so we don’t really expect to do much better.

---

More notes from the lecture notes…

Pseudocode:

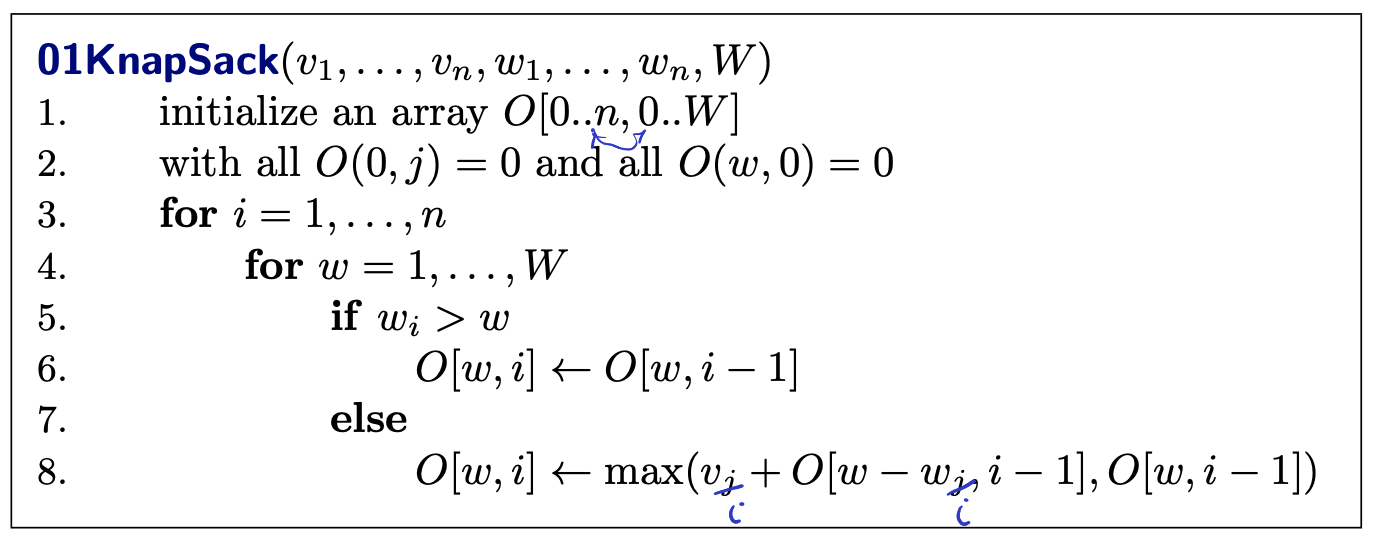
• Doesn’t show how to recover the solution in this pseudocode!
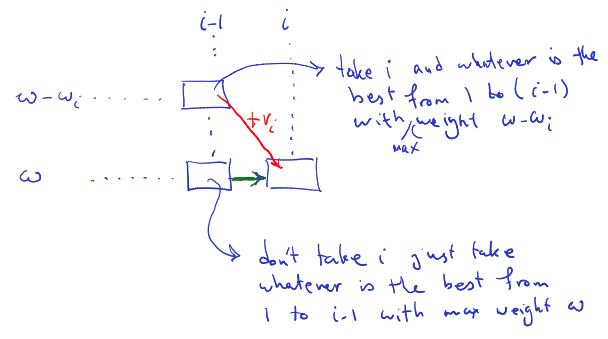
• Update maximum value: If the weight of the current item is less than or equal to the current capacity, we have two choices: either include the current item or exclude it. We choose the option that maximizes the value. The maximum value achievable considering the current item is calculated as the maximum of two values:
  • $v_i+O[w-w_i,i-1]$: Value of the current item plus the maximum value achievable with the remaining capacity $w-w_i$​ and considering only the items up to $i-1$.to-understand
    • $v_i$: current value of item $i$, that we are considering including or not.
    • $O(w-w_i,i-1)$: represents the maximum value achievable with the remaining capacity $w-w_i$ and considering only the tiems up to $(i-1)$-th item. It’s the max value achievable with the remaining capacity $w-w_i$, if we decide to include item $i$ in the knapsack. We consider only the items from the first to the $(i-1)$-th item because we have already made a decision about including item $i$. We cannot include the same item more than once in the 0/1 Knapsack Problem, so we only consider the items before $i$.
    • Putting these two terms together, $v_i+O[w-w_i,i-1]$ represents the total value achieved by including item $i$ in the knapsack. It adds the value of item ii to the maximum value achievable with the remaining capacity if item $i$ is included.
    • We compare this value with the maximum value achievable without including item ii, which is $O[w,i-1]$. We choose the maximum of these two values, as it represents the optimal decision for including or excluding item ii in the knapsack.
  • $O[w,i-1]$: Maximum value achievable without including the current item.

Runtime: $\Theta (nW)$

• Something is hidden?
• What is the actual input size? Roughly what are the parameters of the input size? Twice of $n$ so $2n$ and we also have for each of those numbers: $\log (number)$. And also $w$ is given. It is an integer. How many bits you need to store $w$ in memory. = $\log (w)$. Is $\Theta (nW)$ written in terms of input size. NO. Let’s rewrite it in a way we can see the input size: $\Theta (n2\log (w))$.

Prof’s notes:

• 0/1 Knapsack example:

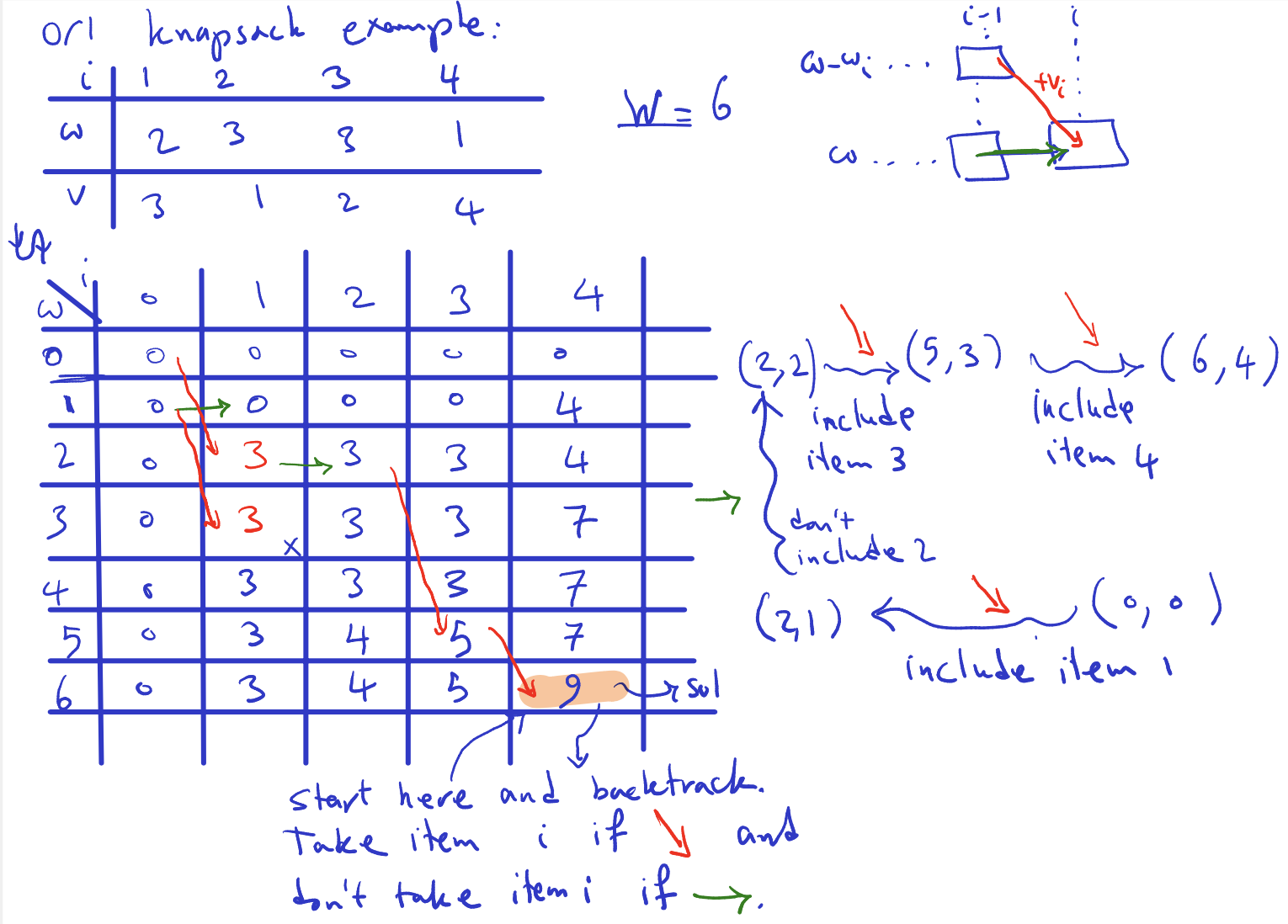
• Base case is first row and column being 0.
• Order of computation: go column by column (make sure to write the order of computation and not just draw arrows on the final exam)
• So check first if we can, if so, then look to the left and also the cell of the row - the value. and whatever in the cell + value?
• Flag those places in $i$ is taken or not: if not taken: taken from left, if taken, then the diagonal is taken.

Make sure to compute the values by yourself later!

• Watch a video on it

He’s keeping track of values in his array!!!