This module covers the LL(1) top-down parsing algorithm for obtaining a derivation for an input string given a CFG. We begin with the start symbol of the grammar and apply production rules until we obtain the input string.

Top-Down $\equiv$ begins at the top of the parse tree and work our way down towards the leaves of the tree which are the terminals in the input string.

Augmented Grammars

We can augment the grammar by creating G’ = (N], T’, P’, S’) from our original CFG = (N, T, P, S).

• Why augment?
  • If a grammar does not satisfy the condition tha tthe starting symbol has only one production rule. $⊢$ and $⊣$ symbolize the beginning and end of the file.
• Why us $⊢$ and $⊣$ ?
  • Very useful since it is not part of the input and when the algorithm read this symbol, they know when the end of input has been reached.

Top-Down Parsing Algorithm

Start by pushing the start symbol of the grammar on the stack. While the TOS is a terminal, pop it and match it against input. If it does not match, report a parse error. Otherwise continue with the next symbol. If TOS is a non-terminal A, pop it and query $Predict[A][a]$where a is the first unmatched symbol from the input. If $Predict[A]|[a]$ has no rule for us, reject with a parse error. Otherwise, if $Predict[A][a]$ returns a rule A → γ, apply the rule by pushing the symbols in γ in reverse. We push the symbols in reverse so that the leftmost symbol ends up on TOS, and therefore, reading from the top of the stack to the bottom gives the symbols of γ in the right order. This also ensures that the first non- terminal we encounter is the leftmost non-terminal (recall we are aiming for leftmost derivations). Repeat until we get a parse error or the stack is empty, at which point we accept. At any given point, the stack contents represent the truncated αi, that is, the current part of the derivation with the matched prefix removed.

Nullable

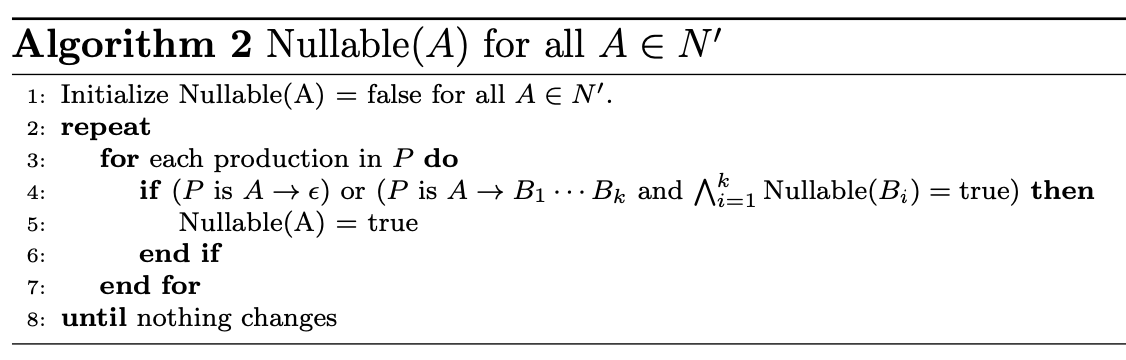A non-terminal A is nullable if it directly derives $ϵ$ or has a rule of the form $A\to B_1\cdot \cdot \cdot B_k$ where each $B_1$ through $B_k$ are nullable.

First

We begin by presenting an algorithm for computing $First(A)$ where $A$ is a non terminal.

This algoirthm computes the First set of an arbitrary $\beta$ (i.e., not necessairy the right hand-side of a rule). Use the following to computate the Follow sets. Look at notes for an example.

Follow

The algorithm goes through each rule A → B1 · · · Bk and updates Follow(Bi) to contain First(Bi+1 · · · Bk ) since First(Bi+1 · · · Bk ) is the set of terminals that can occur as the first symbol in a derivation starting with Bi+1 · · · Bk , which means they can follow Bi . Additionally, $Follow(B_i)$ should also contain the $Follow(A)$ if $B_i$ is the last symbol in the rule or if all symbols after$B_i$ are nullable.

Example in the notes. (Last time I checked, I understand 09/12/2022)

Predict

Predict algorithm with all those newly introduced algorithms. Go through all the predictions, no iteration required. Compute the $First(\beta )$ and $Nullable(\beta )$ .

For the same rule, A → β, we compute Nullable(β) using the Nullable values for non-terminals. If Nullable(β) is true, we add A → β to Predict A a. NOT SURE WHAT THIS MEANS

Parse Trees