Shortest-Path Algorithms

Bellman-Ford Algorithm

Used on directed weighted graphs.

Bellman-Ford is a single source shortest path algorithm that determines the shortest path between a given source vertex and every other vertex in a graph. This algorithm can be used on both weighted and unweighted graphs.

The Bellman–Ford algorithm finds shortest paths from a starting node to all nodes of the graph. (Exactly what is needed in A4Q1)

Instead of using a priority queue as Dijkstra’s Algorithm, Bellman-Ford’s algorithm relaxes all the edges, and does this $|V|-1$ times, where $|V|$ is the number of vertices.

• First line: the algorithm initializes the distance to the source to 0 and all other nodes to infinity
• Then we initialize an array parent (also called predecessor)
• Then for all edges, if the distance to the destination can be shortened by taking the edge, the distance is updated to the new lower value
• The core of the algorithm is a loop that scans across all edges at every loop.
• For every $i\le |V|-1$, at the end of the $i$-th iteration, from any vertex $v$, following the predecessor trail recorded in predecessor yields a path that has a total weight that is at most $distance[v]$, and further, $distance[v]$ is a lower bound to the length of any path from source to $v$ that uses at most $i$ edges.

A common improvement when implementing the algorithm is to return early when an iteration of step 2 fails to relax any edges, which implies all shortest paths have been found, and therefore there are no negative cycles. In that case, the complexity of the algorithm is reduced from $O(|V|\times |E|)$ where $O(l\times |E|)$ is the maximum length of a shortest path in the graph.

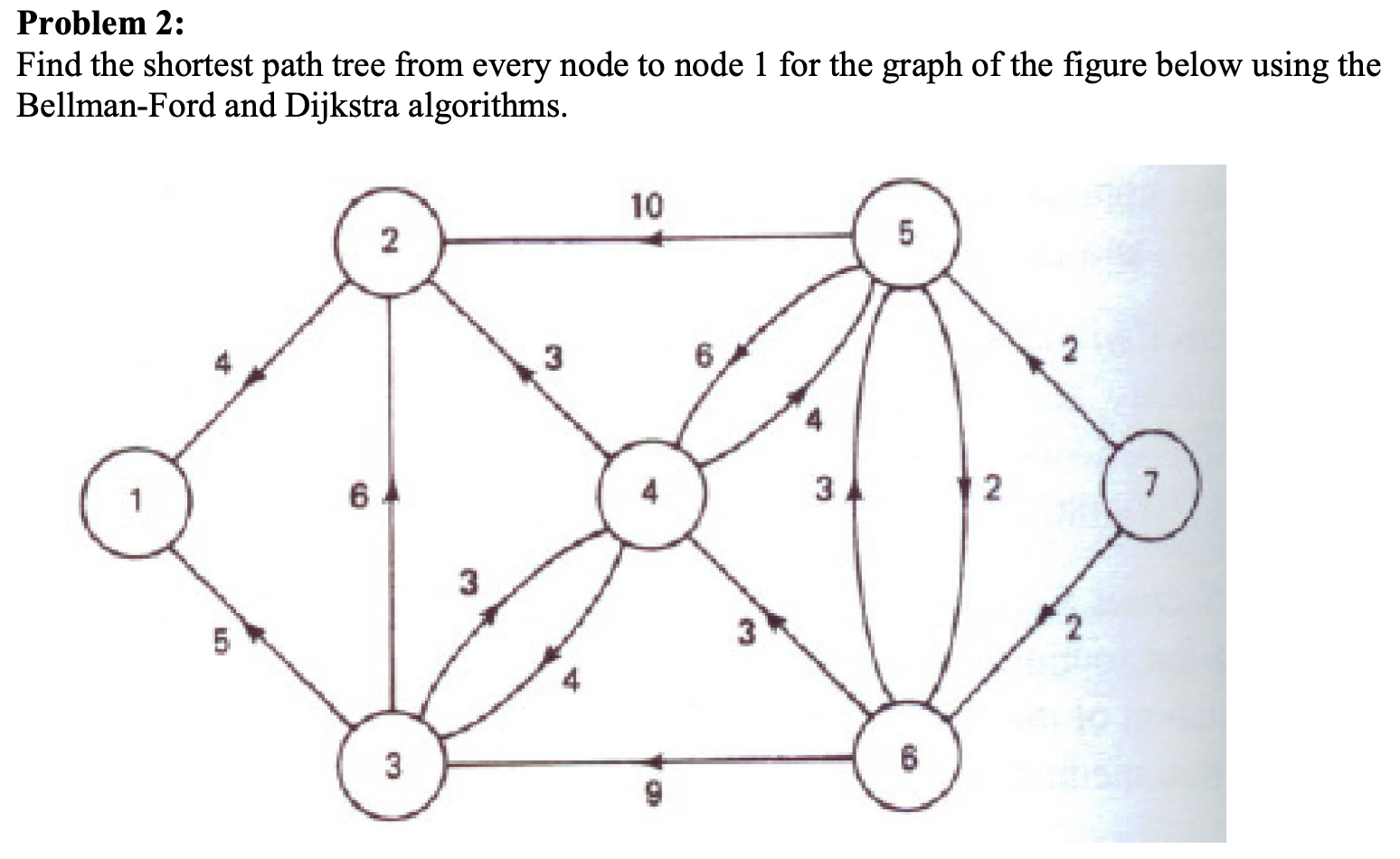
Example

Answer: