Binary Search Tree

A binary search tree is a specific type of binary tree where each left child of a node has a value that is less than the parent and the right child has a greater value than the parent.

BST as a realization of ADT Dictionary.

BST Search(k): Start at root and compare k to current’s node’s key. Stop if found or subtree is empty, else recurse at subtree.

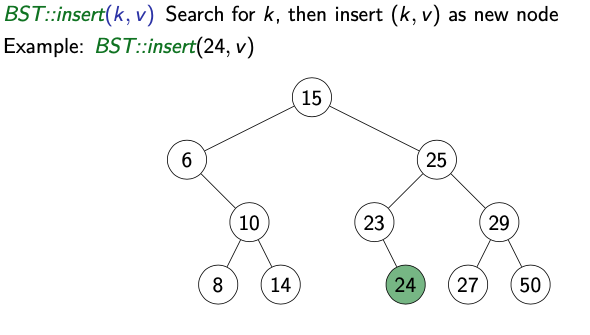
BST Insert(k, v): Search for k, then insert (k, v) as new node.

BST Delete(k):

• First search for the node x that contains the key
• If x is a leaf(both subtrees are empty), delete it
• If x has one non-empty subtree, move child up
• Else, swap key at x with a key at successor or predecessor node and then delete that node

Complexity Analysis

All BST Search, Insert and Delete have cost $\Theta (h)$, where $h=$ height of the tree $=$ max. path length from root to leaf.