Korasaju’s Algorithm

Is a linear time algorithm to find the strongly connected components of a directed graph.

Definition: for a Directed Graph $G=(V,E)$, the reverse (or transpose) graph $G^T=(V,E^T)$ is the graph with same vertices, and reversed edges.

Basically run DFS twice.

You can always turn directed graphs into SCCs

Consider the case where we just have vertices and zero edges. Every vertex itself is a SCC. Then if we add edges, it is possible we create a larger SCC, thus decreasing the number of them. Note that the minimum number of SCCs (assuming at least one vertex exists) is 1. That case is when every vertex is connected with each other.

Complexity: $O(n+m)$ (don’t forget the time to reverse $G$)

Exercise: check that the strongly connected components of $G$ and $G^T$ are the same.

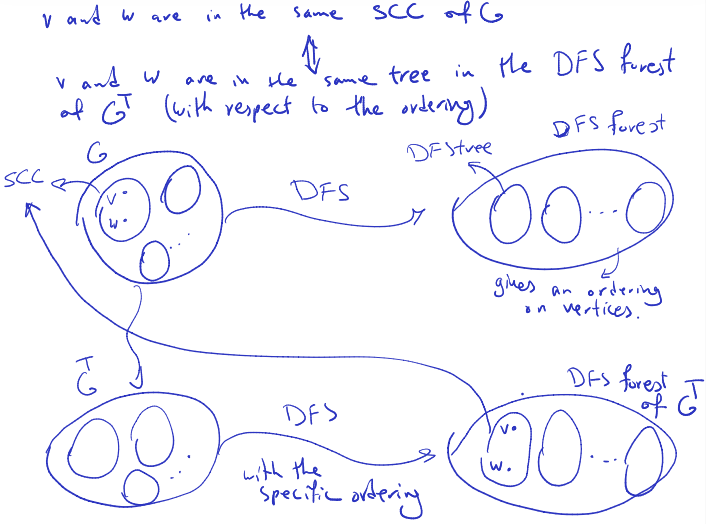
Correctness Want to prove: for any vertices $v,w$, the following are equivalent:

1. $v$ and $w$ are in the same strongly connected components of $G$
2. $v$ and $w$ are in the same tree in the DFS forest of $G^T$ (with vertices ordered in decreasing finish time)

Proof of 1 $\Rightarrow$ 2 (order of the vertices does not matter here).

Let $C$ be the strongly connected component of $G$ that contains $v$ and $w$.

Another question:

Apparently $G^{\prime }$ is always a DAG. $\to$ Start with a graph $G$, next compute the SCCs of $G$. We construct a graph $G^{\prime }$, whose vertex set is the SCCs of $G$, and we add a directed edge from an SCC $V_i$ to an SCC $V_j$ if and only if there exist vertices $v_i\in V_{i,}$ $v_{j\in }{V}_j$ such that $(v_{i,}{v}_j)$ is an edge in $G$. The claim is that $G^{\prime }$ is a DAG.